Os problema são sobre séries. Os enunciados são os seguintes:
"Determine o termo geral da seguinte série: 3/2+(3*5)/(2*4)+(3*5*7)/(2*4*6)+... "
ainda não adiantei muito do problema, só cheguei ainda a uma conclusão simples, precisava de uma ajudita...
a solução deve ter por base qualquer coisa como o somatório de n=1 ate infinito dos termos dados pela expressao (2n+1)/(2n)
"Seja
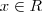 . Qual a condição necessária e suficiente sobre x para que a série
. Qual a condição necessária e suficiente sobre x para que a série 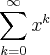 seja convergente? No caso em que a série é convergente, encontre a sua soma."
seja convergente? No caso em que a série é convergente, encontre a sua soma."Estava a pensar assumir que x deveria ser igual a 0 para a série ser convergente, mas não tenho a certeza.
Desde já obrigada a quem responder à minhas dúvidas =)


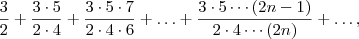



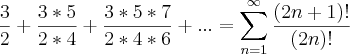 pois não?
pois não?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)