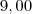locadora de carros

[maria cleide]

Uma locadora de carros A cobra reais por quilômetro rodado e uma taxa adicional de 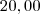reais. Uma locadora B cobra 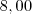reais por quilômetro rodado, uma taxa adicional de 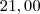e, ainda, 10% sobre o total. A partir de quantos quilômetros rodados a locadora B é mais vantajosa?
A-( )14Km
B-( )15,5Km
C-( )10,5Km
D-( )12Km
E-( )18Km


Como fiz:
1KM:A)20,00+9,00=29,00
B)21,00+8,00+10%=31,90 (DIFERENÇA DE 2,90)

2KM:
A)18,00+20,00=38,00
B)26,00+21,00+10%=40,70(DIFERENÇA DE 2,70)

3KM:
A)27,00+20,00=47,00
B)26,00+21,00+10%=49,50(DIFERENÇA DE 2,50)

4KM:
A)36,00+20,00=56,00
B)32,00+21,00+10%=58,30(DIFERENÇA DE 2,30)

5KM:
A)45,00+20,00=65,00
B)40,00+21,00+10%=67,10

14KM:
A)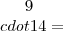126,00+20,00=146,00
B)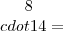112,00+21,00+10%=146,30(DIFERENÇA DE 0,30)

15KM:
A)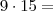135,00+20,00=155,00
B)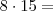120,00+21,00+10%=155,10(DIFERENÇA DE 0,10)

15,5KM:

A)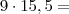139,50+20,00=159,50
B)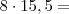124,00+21,00+10%=159,50(EMPATE).

Resolvi deste modo, mas não existe uma forma mais fácil de encontrar a resposta?

[norberto]

Oi cleide !

Na verdade tem. Generalizando.

Considere que podemos chamar "quilômetros rodados" de x

i. A = 9x + 20

ii. B = 8x + 21 + 10%(8x + 21) ---> B = 8,8x + 2,1

iii. B é mais vantajoso quando B < A ou melhor, quando :

8,8x + 2,1 < 9x + 20


Quando você resolver, vai chegar em :

15,5 < x

Que é mesmo que :

x > 15,5


Abraços

PS:

Lembre-se que esse problema é de "ÁLGEBRA" e não de "SEQUÊNCIAS"

[norberto]

Oi cleide !

Desculpe, mas cometi um engano. É que não digitei um "3" importante.


ii. B = 8x + 21 + 10%(8x + 21) ----> B = 8,8x + 23,1

Abraços.