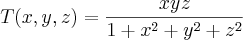
a) Determine a taxa de variação da temperatura no ponto (1,1,1) na direção e sentido à origem.
b) Determine a direção e o sentido em que a temperatura cresce mais rapidamente a partir do ponto (1,1,1).
c) Determine a taxa de variação da temperatura no ponto (1,1,1), na direção e no sentido obtido no item b.
Bom, só consegui fazer a letra a. Calculei o vetor gradiente e multipliquei pelo ponto dado.
Mas não estou conseguindo fazer os outros itens.
Poderiam me ajudar?




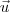 um vetor unitário. Então pela definição de taxa de variação (ou derivada direcional) temos que
um vetor unitário. Então pela definição de taxa de variação (ou derivada direcional) temos que  .
.  , pois
, pois 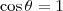 . Portanto a taxa de variação na direção máxima faz ângulo zero com o vetor gradiente, ou seja, é o próprio vetor gradiente, e seu valor é
. Portanto a taxa de variação na direção máxima faz ângulo zero com o vetor gradiente, ou seja, é o próprio vetor gradiente, e seu valor é 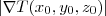 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

