 por Henrique Bueno » Qua Jun 20, 2012 16:37
por Henrique Bueno » Qua Jun 20, 2012 16:37
O exercício é o seguinte:
Prove que
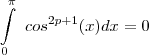
com p pertencente a Z.
(sugestão: faça
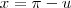
)
eu tentei usar a sugestão e cai na mesma coisa de antes porém na variável u. Tentei dizer que u=senx e encontrei a seguinte integral:
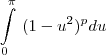
porém dai eu não consigo sair. Por favor, me ajudem!
-
Henrique Bueno
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 02, 2011 19:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Jun 20, 2012 21:29
por Russman » Qua Jun 20, 2012 21:29
A demonstração é relativamente simples. Veja que efetuando a mudança de variável temos
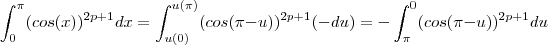
.
Agora utilizando a propriedade de inversão de limites de integração e o fato que
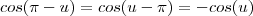
, temos , portanto
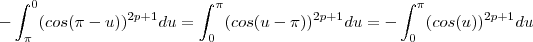
,
uma vez que o sinal de menos sobrevive as potências ímpares.
Agora veja que, do início,
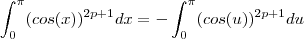
.
Note que

e

são, nos processos de integração, variáveis "mudas", isto é, como efetua-se uma integração definida as variáveis, no resultado final, não aparecem explicitamente. Logo, podemos tomar
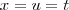
. Assim,
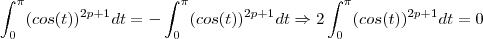
.
e, portanto,
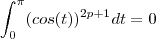
c.q.d
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8866 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- DEMONSTRAÇÃO
por arima » Seg Nov 08, 2010 08:40
- 8 Respostas
- 5932 Exibições
- Última mensagem por roseli

Qua Nov 10, 2010 21:03
Álgebra Elementar
-
- Demonstração
por Lorettto » Qui Dez 16, 2010 23:03
- 3 Respostas
- 2271 Exibições
- Última mensagem por Elcioschin

Seg Dez 20, 2010 12:39
Álgebra Elementar
-
- Demonstração
por Pedro2 » Sáb Mar 12, 2011 15:38
- 1 Respostas
- 1961 Exibições
- Última mensagem por Guill

Sex Abr 20, 2012 16:01
Matrizes e Determinantes
-
- PA - Demonstração
por jessicaccs » Sex Mar 25, 2011 11:52
- 1 Respostas
- 1472 Exibições
- Última mensagem por Elcioschin

Sex Mar 25, 2011 14:55
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
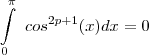 com p pertencente a Z.
com p pertencente a Z.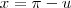 )
)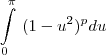

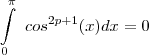 com p pertencente a Z.
com p pertencente a Z.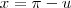 )
)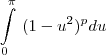

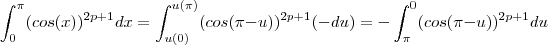 .
.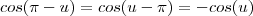 , temos , portanto
, temos , portanto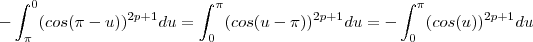 ,
,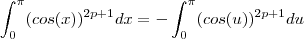 .
. e
e  são, nos processos de integração, variáveis "mudas", isto é, como efetua-se uma integração definida as variáveis, no resultado final, não aparecem explicitamente. Logo, podemos tomar
são, nos processos de integração, variáveis "mudas", isto é, como efetua-se uma integração definida as variáveis, no resultado final, não aparecem explicitamente. Logo, podemos tomar 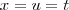 . Assim,
. Assim,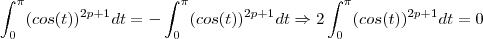 .
.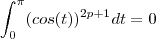

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.