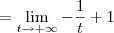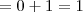por edu2012 » Ter Mai 29, 2012 16:38
por edu2012 » Ter Mai 29, 2012 16:38
Boa tarde, gostaria de um exemplo de integral imprópria quando ela converge ou Diverge até agora não estou entendendo.
um exemplo
?
? x+1/(x²+2x) dx
1
desde de já agradeço.
-
edu2012
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 29, 2012 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica
- Andamento: cursando
 por LuizAquino » Ter Mai 29, 2012 20:53
por LuizAquino » Ter Mai 29, 2012 20:53
edu2012 escreveu:Boa tarde, gostaria de um exemplo de integral imprópria quando ela converge ou Diverge até agora não estou entendendo.
um exemplo
?
? x+1/(x²+2x) dx
1
Do jeito que você escreveu, a integral seria:
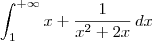
Mas ao que parece, a integral original seria:

Se esse for o caso, então você deveria ter escrito algo como:
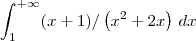
Note a importância do uso adequado dos parênteses.
Supondo que essa seja a integral que você deseja calcular, a primeira coisa que você precisa fazer é resolver a integral indefinida. Nesse caso, você irá obter:
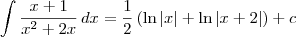
Depois que você resolveu a integral indefinida, você pode partir para resolver a integral imprópria. Você deve seguir o seguinte procedimento:
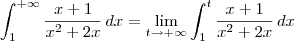
![= \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t = \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t](/latexrender/pictures/5254ecef9540c8883a9438aca418ea60.png)
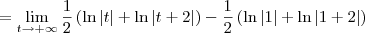
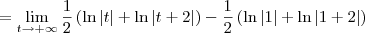
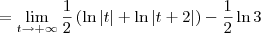
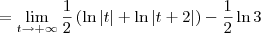
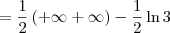

Como o resultado da integral imprópria foi infinito, temos que ela é divergente.
Se no final dos cálculos você tivesse encontrado como resultado um valor fixo, então a integral imprópria seria convergente. Por exemplo, considere a seguinte integral imprópria:
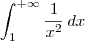
Note que:

Sendo assim, temos que:
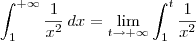
![= \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t = \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t](/latexrender/pictures/765779293a3854676a11157002910beb.png)

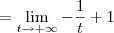
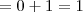
Como o resultado da integral imprópria foi um valor fixo, temos que ela é convergente. Nesse caso, diremos que essa integral imprópria converge para 1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por edu2012 » Qua Mai 30, 2012 09:24
por edu2012 » Qua Mai 30, 2012 09:24
Luis Aquino Obrigado.
-
edu2012
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 29, 2012 15:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6489 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- Calculo 2 AJUDA
por rodrigojuara » Seg Jun 15, 2015 23:38
- 0 Respostas
- 7439 Exibições
- Última mensagem por rodrigojuara

Seg Jun 15, 2015 23:38
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Ajuda
por leandrofsm » Qui Jan 05, 2017 14:59
- 1 Respostas
- 10962 Exibições
- Última mensagem por Cleyson007

Ter Jan 10, 2017 17:56
Cálculo
-
- Ajuda com Calculo (?)
 por opb1212 » Qui Ago 31, 2017 20:32
por opb1212 » Qui Ago 31, 2017 20:32
- 0 Respostas
- 1271 Exibições
- Última mensagem por opb1212

Qui Ago 31, 2017 20:32
Cálculo: Limites, Derivadas e Integrais
-
- exercício calculo do VAL Ajuda
por nhrd » Qui Dez 11, 2008 23:20
- 0 Respostas
- 2231 Exibições
- Última mensagem por nhrd

Qui Dez 11, 2008 23:20
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



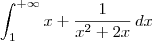

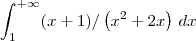
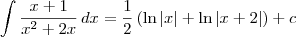
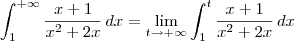
![= \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t = \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t](/latexrender/pictures/5254ecef9540c8883a9438aca418ea60.png)
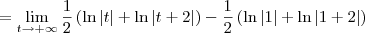
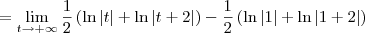
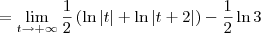
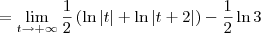
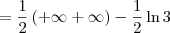

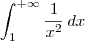

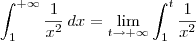
![= \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t = \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t](/latexrender/pictures/765779293a3854676a11157002910beb.png)