 por panneitz » Dom Jun 07, 2009 19:55
por panneitz » Dom Jun 07, 2009 19:55
Preciso de ajuda, pois passei o domingo tentando fazer e não consegui, por isso estou postando aqui.
1 - Calcule:
![\int_{1}^{0}\sqrt[5]{{x}^{2}}\ dx \int_{1}^{0}\sqrt[5]{{x}^{2}}\ dx](/latexrender/pictures/d4035ebbee693e38143b2ce4a4183a30.png)
2 - Calcule a integral da função:
![f(x)={e}^{x}+ 5 +\sqrt[]{x} f(x)={e}^{x}+ 5 +\sqrt[]{x}](/latexrender/pictures/18d1031d581caecec0d8317c8ad5c5b1.png)
3 - Calcule a integral da função:
![f(x)=(2cosx+ \frac{1}{\sqrt[ ]{x}})dx f(x)=(2cosx+ \frac{1}{\sqrt[ ]{x}})dx](/latexrender/pictures/78bb58afddb765edda6352e82fd7c8e5.png)
Preciso dos exemplos para estudar a maneira de proceder com estes cálculos.
Desde já agradeço.
-
panneitz
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 05, 2009 22:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Marcampucio » Dom Jun 07, 2009 20:31
por Marcampucio » Dom Jun 07, 2009 20:31
Integrais são resolvidas por fórmulas de integração. Antes de mais nada você precisa de um formulário. Vou deixar um link
Regras de Integração-clique aqui1-
![\int_0^1{\sqrt[5]{x^2}dx=\int_0^1{x^{\frac{2}{5}}=\int_0^1{x^n}=\frac{x^{n+1}}{n} \int_0^1{\sqrt[5]{x^2}dx=\int_0^1{x^{\frac{2}{5}}=\int_0^1{x^n}=\frac{x^{n+1}}{n}](/latexrender/pictures/ac48fbb9b6ae8768deca5f505ae64db6.png)
![\int_0^1{\sqrt[5]{x^2}dx=\frac{5x^{\frac{7}{5}}}{2}/_0^1=\frac{5}{2} \int_0^1{\sqrt[5]{x^2}dx=\frac{5x^{\frac{7}{5}}}{2}/_0^1=\frac{5}{2}](/latexrender/pictures/597e5c47b24adb6dd46f4e1108432a81.png)
2-
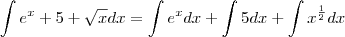
experimente fazer esta. Use o formulário. Coloque suas tentativas se tiver dúvidas.
3-
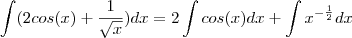
tá fácil. Use as regras.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8866 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2816 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2534 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2139 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por Bruhh » Sáb Ago 07, 2010 14:49
- 3 Respostas
- 3234 Exibições
- Última mensagem por Molina

Dom Ago 08, 2010 15:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{0}\sqrt[5]{{x}^{2}}\ dx \int_{1}^{0}\sqrt[5]{{x}^{2}}\ dx](/latexrender/pictures/d4035ebbee693e38143b2ce4a4183a30.png)
![f(x)={e}^{x}+ 5 +\sqrt[]{x} f(x)={e}^{x}+ 5 +\sqrt[]{x}](/latexrender/pictures/18d1031d581caecec0d8317c8ad5c5b1.png)
![f(x)=(2cosx+ \frac{1}{\sqrt[ ]{x}})dx f(x)=(2cosx+ \frac{1}{\sqrt[ ]{x}})dx](/latexrender/pictures/78bb58afddb765edda6352e82fd7c8e5.png)

![\int_{1}^{0}\sqrt[5]{{x}^{2}}\ dx \int_{1}^{0}\sqrt[5]{{x}^{2}}\ dx](/latexrender/pictures/d4035ebbee693e38143b2ce4a4183a30.png)
![f(x)={e}^{x}+ 5 +\sqrt[]{x} f(x)={e}^{x}+ 5 +\sqrt[]{x}](/latexrender/pictures/18d1031d581caecec0d8317c8ad5c5b1.png)
![f(x)=(2cosx+ \frac{1}{\sqrt[ ]{x}})dx f(x)=(2cosx+ \frac{1}{\sqrt[ ]{x}})dx](/latexrender/pictures/78bb58afddb765edda6352e82fd7c8e5.png)

![\int_0^1{\sqrt[5]{x^2}dx=\int_0^1{x^{\frac{2}{5}}=\int_0^1{x^n}=\frac{x^{n+1}}{n} \int_0^1{\sqrt[5]{x^2}dx=\int_0^1{x^{\frac{2}{5}}=\int_0^1{x^n}=\frac{x^{n+1}}{n}](/latexrender/pictures/ac48fbb9b6ae8768deca5f505ae64db6.png)
![\int_0^1{\sqrt[5]{x^2}dx=\frac{5x^{\frac{7}{5}}}{2}/_0^1=\frac{5}{2} \int_0^1{\sqrt[5]{x^2}dx=\frac{5x^{\frac{7}{5}}}{2}/_0^1=\frac{5}{2}](/latexrender/pictures/597e5c47b24adb6dd46f4e1108432a81.png)
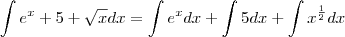
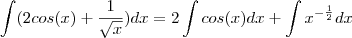



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.