O enunciado do exercício é: calcule a derivada total da seguinte função:
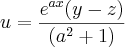 , sendo y =a sen(x) e z= cos(x), com a constante. Está indicado como solução
, sendo y =a sen(x) e z= cos(x), com a constante. Está indicado como solução 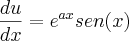 .
.No entanto, segundo a minha resolução, não consigo chegar ao resultado apresentado.
Segue agora como resolvi:
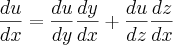 .
.ora,
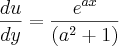
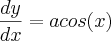
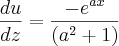
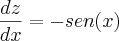
Logo,
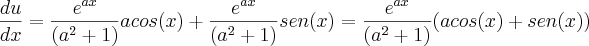
Muito provavelmente, é necessário fazer simplificações e/ou substituições para chegar à solução dada, mas de momento não estou a ver como.
Peço ajuda.
Obrigado!


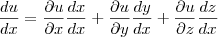

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)