O enunciado do exercício é: calcule a derivada total da seguinte função:
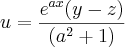 , sendo y =a sen(x) e z= cos(x), com a constante. Está indicado como solução
, sendo y =a sen(x) e z= cos(x), com a constante. Está indicado como solução 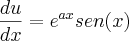 .
.No entanto, segundo a minha resolução, não consigo chegar ao resultado apresentado.
Segue agora como resolvi:
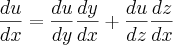 .
.ora,
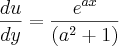
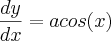
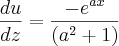
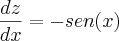
Logo,
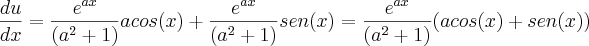
Muito provavelmente, é necessário fazer simplificações e/ou substituições para chegar à solução dada, mas de momento não estou a ver como.
Peço ajuda.
Obrigado!


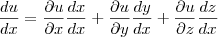


 .
.
 :
: