pedcoi escreveu:Calcule a área da região do plano delimitada pelas linhas:
y=cos(?x) y=1-2x
pedcoi escreveu:Eu sei que tenho que igualar a primeira expressão com a segunda, e descobrir os pontos de intersecção, fazendo depois o integral.
Ok.
pedcoi escreveu:Mas o meu problema é como conseguir resolver a expressão cos(?x) = 1-2x. O cos confunde-me.
Esta é uma
equação transcendental. Isso significa que não há uma forma analítica conhecida de se resolver. Ou seja, você precisa utilizar alguma estratégia numérica. Nesse caso, você pode resolver por inspeção. Isto é, substituir valores convenientes em x e verificar se a igualdade vale.
Pois bem, comece procurando por soluções triviais. Que nesse caso são x = 0, x=1/2 e x = 1.
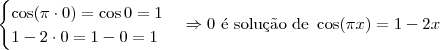
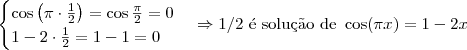

Agora tente terminar o exercício.


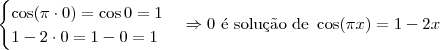
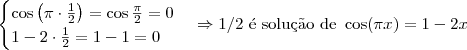



 .
.
 :
: