 por ah001334 » Ter Dez 20, 2011 10:47
por ah001334 » Ter Dez 20, 2011 10:47
Pessoa vejam essa questão, eu fiz e a professora me deu errado não sei pq para mim esta correto
Determine o volume de um sólido formado pela revolução em torno do eixo y, da região delimitada pelo gráfico de y=x³ limitada por y=8 e x=0
![v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2} v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2}](/latexrender/pictures/384d675a6a8ccddbcd6090600e24cacd.png)
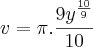
![v= \pi.\left[9.\frac{{8}^{{10}^{9}}}{10}-9.\frac{{0}^{\frac{10}{9}}}{10}\right] v= \pi.\left[9.\frac{{8}^{{10}^{9}}}{10}-9.\frac{{0}^{\frac{10}{9}}}{10}\right]](/latexrender/pictures/7ba282db828a592a28c8c509fd70c7fc.png)
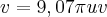
em torno de y
y=8
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Ter Dez 20, 2011 11:24
por LuizAquino » Ter Dez 20, 2011 11:24
ah001334 escreveu:Determine o volume de um sólido formado pela revolução em torno do eixo y, da região delimitada pelo gráfico de y=x³ limitada por y=8 e x=0
ah001334 escreveu:Pessoa vejam essa questão, eu fiz e a professora me deu errado não sei pq para mim esta correto (...)
![v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2} v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2}](/latexrender/pictures/384d675a6a8ccddbcd6090600e24cacd.png)
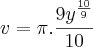
Note que:
![\pi \int \left(\sqrt[3]{y}\right)^2\,dy = \frac{3\pi}{5}y^{\frac{5}{3}} + c \pi \int \left(\sqrt[3]{y}\right)^2\,dy = \frac{3\pi}{5}y^{\frac{5}{3}} + c](/latexrender/pictures/7a81726d336f498dfa06b5884a5ea653.png)
Agora reveja a sua solução.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Volume do Solido
por leha » Qui Dez 10, 2009 10:22
- 3 Respostas
- 3395 Exibições
- Última mensagem por leha

Seg Dez 14, 2009 13:44
Cálculo: Limites, Derivadas e Integrais
-
- Volume de sólido
 por Manoella » Seg Fev 21, 2011 23:41
por Manoella » Seg Fev 21, 2011 23:41
- 1 Respostas
- 2473 Exibições
- Última mensagem por LuizAquino

Ter Fev 22, 2011 11:38
Cálculo: Limites, Derivadas e Integrais
-
- volume de um sólido
 por Andreza » Seg Nov 14, 2011 14:26
por Andreza » Seg Nov 14, 2011 14:26
- 7 Respostas
- 8556 Exibições
- Última mensagem por Andreza

Sex Nov 25, 2011 10:05
Geometria Espacial
-
- volume de um sólido
por Priscila_moraes » Dom Dez 04, 2011 18:55
- 2 Respostas
- 2734 Exibições
- Última mensagem por LuizAquino

Dom Dez 04, 2011 19:56
Cálculo: Limites, Derivadas e Integrais
-
- Volume do solido
por ivoski » Ter Ago 14, 2012 17:38
- 2 Respostas
- 2696 Exibições
- Última mensagem por ivoski

Qui Ago 16, 2012 22:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2} v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2}](/latexrender/pictures/384d675a6a8ccddbcd6090600e24cacd.png)
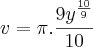
![v= \pi.\left[9.\frac{{8}^{{10}^{9}}}{10}-9.\frac{{0}^{\frac{10}{9}}}{10}\right] v= \pi.\left[9.\frac{{8}^{{10}^{9}}}{10}-9.\frac{{0}^{\frac{10}{9}}}{10}\right]](/latexrender/pictures/7ba282db828a592a28c8c509fd70c7fc.png)
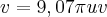

![v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2} v= \pi.\int_{8}^{0}\left(\sqrt[3]{y} \right){}^{2}](/latexrender/pictures/384d675a6a8ccddbcd6090600e24cacd.png)
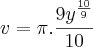
![v= \pi.\left[9.\frac{{8}^{{10}^{9}}}{10}-9.\frac{{0}^{\frac{10}{9}}}{10}\right] v= \pi.\left[9.\frac{{8}^{{10}^{9}}}{10}-9.\frac{{0}^{\frac{10}{9}}}{10}\right]](/latexrender/pictures/7ba282db828a592a28c8c509fd70c7fc.png)
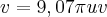

![\pi \int \left(\sqrt[3]{y}\right)^2\,dy = \frac{3\pi}{5}y^{\frac{5}{3}} + c \pi \int \left(\sqrt[3]{y}\right)^2\,dy = \frac{3\pi}{5}y^{\frac{5}{3}} + c](/latexrender/pictures/7a81726d336f498dfa06b5884a5ea653.png)
