 por -civil- » Qui Set 29, 2011 14:12
por -civil- » Qui Set 29, 2011 14:12
Intua o valor do limite abaixo, usando caminho. Depois prove pela definição que o limite é o que você intuiu, deixando claro as etapas: o projeto de  em função de
em função de  , o valor do
, o valor do  e finalmente a confirmação de
e finalmente a confirmação de  .
.
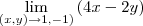
Eu resolvi assim:
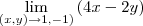
=
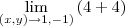
= 8
(Posso considerar que esse é um jeito de resolver por caminho?)
Seja

> 0, queremos achar

tal que |4x - 2y| <

sempre que
0 <
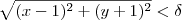
0 <
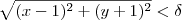
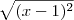
= | x - 1 | <
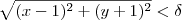
--->>>> projeto de


= | y + 1| <
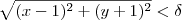
|4x - 4 -2y - 2 + 6 | <

|4(x-1) - 2(y+1) + 6 | <

|4(x-1) - 2(y+1) | <

4|x-1| - 2|y+1| <

(Eu posso fazer isso, tendo um sinal negativo ali no meio????)
4

- 2

<

2

<

valor de

:
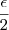
confirmação do

:
Suponhamos que 0 <
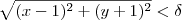
então
| x - 1 | <

e | y + 1| <

Assim:
4|x-1| - 2|y+1| < 4

- 2

< 2

4|x-1| - 2|y+1| <
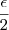
Como |4(x-1) - 2(y+1)|

4|x-1| - 2|y+1|
então
|3(x-1) + 2(y+1)| <

Está correta a minha resolução?
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sex Set 30, 2011 12:54
por LuizAquino » Sex Set 30, 2011 12:54
-civil- escreveu:Eu resolvi assim:
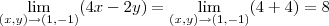
(Posso considerar que esse é um jeito de resolver por caminho?)
Claro que
não! Afinal de contas, você
não especificou que caminho você está seguindo!
Uma forma seria, por exemplo, considerar que você vai se aproximar do ponto (1, -1) seguindo a trajetória da reta y = -x. Note que seguindo essa trajetória, quando x se aproxima de 1, temos que y se aproxima de -1. Sobre essa trajetória, o limite acima é o mesmo que:
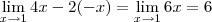
-civil- escreveu:Seja
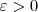
, queremos achar

tal que
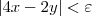
sempre que
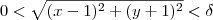
Não é isso. Considerando que você desconfia que o limite seja igual a 6, então o que você quer é tentar provar que:
Seja 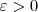 , queremos achar
, queremos achar 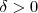 tal que
tal que 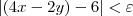 sempre que
sempre que 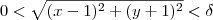 .
.-civil- escreveu: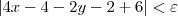
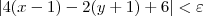
Não é isso. O que temos é:
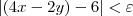

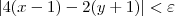
Mas pela desigualdade triangular, sabemos que:
![|4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)| |4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)|](/latexrender/pictures/65718870a2911ba6c60a0626854e02d7.png)
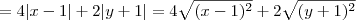
Em resumo, temos que:
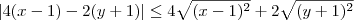
Por outro lado, sabemos que:
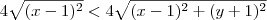
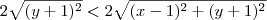
Ou seja, é válido que:
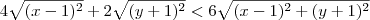
Desse modo, podemos afirmar que:
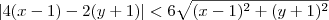
Isso significa que podemos escolher
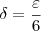
.
Agora, verifique que essa escolha é conveniente.
Observação-civil- escreveu: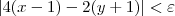
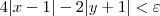
(Eu posso fazer isso, tendo um sinal negativo ali no meio????)
Ao que parece, você executou esse passo pensando que é válido a propriedade |a - b| = |a| - |b|, para quaisquer a e b reais. Entretanto, isso é claramente inválido. Escolha, por exemplo, a = 1 e b = -1. Você perceberá que essa relação é inválida para essa escolha.
A propriedade que de fato nós temos é

, para quaisquer a e b reais . Para uma demonstração dessa propriedade, vide o tópico:
Re: Módulo.viewtopic.php?f=120&t=4101#p13503Considerando agora essa propriedade, se tivermos algo do tipo
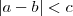
(com
c positivo e não nulo), como

, então podemos afirmar que:
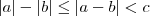
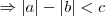
Em resumo, devido a essa propriedade, para quaisquer a, b e c reais (com c positivo e não nulo) temos que:
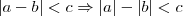
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Demonstrando um limite pela definição
por lucasvier4 » Qui Abr 16, 2015 22:46
- 1 Respostas
- 1532 Exibições
- Última mensagem por adauto martins

Sáb Abr 18, 2015 12:25
Cálculo: Limites, Derivadas e Integrais
-
- Limite pela definição
por -civil- » Qui Mai 26, 2011 02:37
- 5 Respostas
- 3104 Exibições
- Última mensagem por LuizAquino

Qui Mai 26, 2011 13:31
Cálculo: Limites, Derivadas e Integrais
-
- Duvida num limite pela definição
 por TheoFerraz » Qua Abr 13, 2011 19:52
por TheoFerraz » Qua Abr 13, 2011 19:52
- 5 Respostas
- 4016 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 00:52
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição de limite
por SheylaTamarossi » Dom Jun 12, 2011 11:27
- 6 Respostas
- 8331 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 13, 2011 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição de limite
por Andreyan » Ter Jul 12, 2011 17:55
- 4 Respostas
- 2822 Exibições
- Última mensagem por LuizAquino

Qua Jul 13, 2011 15:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 em função de
em função de  , o valor do
, o valor do  e finalmente a confirmação de
e finalmente a confirmação de  .
.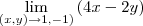
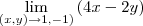 =
= 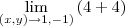 = 8
= 8 > 0, queremos achar
> 0, queremos achar  tal que |4x - 2y| <
tal que |4x - 2y| <  sempre que
sempre que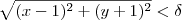
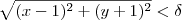
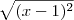 = | x - 1 | <
= | x - 1 | < 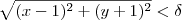 --->>>> projeto de
--->>>> projeto de 
 = | y + 1| <
= | y + 1| < 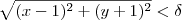



 (Eu posso fazer isso, tendo um sinal negativo ali no meio????)
(Eu posso fazer isso, tendo um sinal negativo ali no meio????) - 2
- 2 <
< 
 <
< 
 :
: 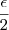
 :
: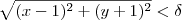 então
então e | y + 1| <
e | y + 1| < 
 - 2
- 2 < 2
< 2
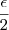
 4|x-1| - 2|y+1|
4|x-1| - 2|y+1|


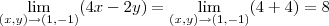
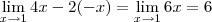
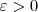 , queremos achar
, queremos achar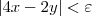 sempre que
sempre que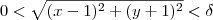
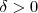 tal que
tal que 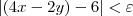 sempre que
sempre que 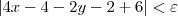
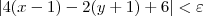

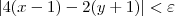
![|4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)| |4(x-1) + [-2(y+1)]| \leq |4(x-1)| + |-2(y+1)|](/latexrender/pictures/65718870a2911ba6c60a0626854e02d7.png)
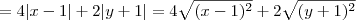
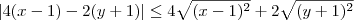
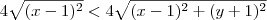
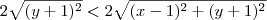
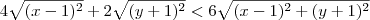
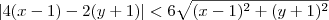
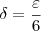 .
.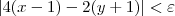
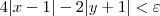
 , para quaisquer a e b reais . Para uma demonstração dessa propriedade, vide o tópico:
, para quaisquer a e b reais . Para uma demonstração dessa propriedade, vide o tópico: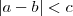 (com
(com  , então podemos afirmar que:
, então podemos afirmar que: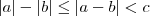
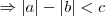
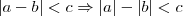

 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: