 por beel » Ter Set 06, 2011 12:08
por beel » Ter Set 06, 2011 12:08
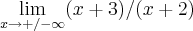
Para achar a assintota horizontal é achar o limite certo?
Nesse caso, meu limite deu +

... isso quer dizer que não existem assintotas horizontais?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Ter Set 06, 2011 12:12
por beel » Ter Set 06, 2011 12:12
Fiz novamente pela regra do polinomio, e deu 1...
Quando eu uso essa "regra"? ( dividir numerador e denominador pelo x^ maior grau do denominador)? sempre que tiver que achar assintotas horizontais?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Set 06, 2011 20:20
por LuizAquino » Ter Set 06, 2011 20:20
isanobile escreveu:Para achar a assintota horizontal é achar o limite certo?
Sim, você deve calcular os limites adequados.
isanobile escreveu:Fiz novamente pela regra do polinomio, e deu 1...
De fato, temos que:
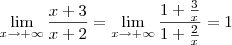
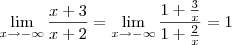
isanobile escreveu:Quando eu uso essa "regra"? ( dividir numerador e denominador pelo x^ maior grau do denominador)? sempre que tiver que achar assintotas horizontais?
Tipicamente você usa essa estratégia quando tem que calcular limites do tipo:
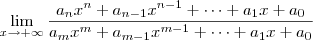
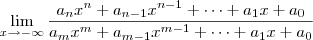
No caso, você deve dividir o numerador e o denominador pelo monômio de maior grau. Por exemplo, se n > m, então você faz a divisão por
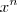
. Mas caso n < m, então você faz a divisão por
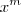
. Obviamente, se n = m tanta faz dividir por qualquer um deles.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Out 16, 2011 16:58
por beel » Dom Out 16, 2011 16:58
Ok,obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ASSINTOTA HORIZONTAL
por iksin » Qua Abr 17, 2019 00:03
- 1 Respostas
- 5977 Exibições
- Última mensagem por Baltuilhe

Qua Mai 01, 2019 17:23
Cálculo: Limites, Derivadas e Integrais
-
- Assintota vertical e horizontal
por Zercamga » Seg Set 17, 2012 12:30
- 6 Respostas
- 10187 Exibições
- Última mensagem por Zercamga

Ter Set 18, 2012 17:32
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida: Assíntota Horizontal de uma função
por Jhonata » Sáb Mai 26, 2012 18:01
- 1 Respostas
- 3134 Exibições
- Última mensagem por MarceloFantini

Dom Mai 27, 2012 15:37
Cálculo: Limites, Derivadas e Integrais
-
- limite {assintota}
por DyegoBrum » Seg Set 19, 2011 13:38
- 1 Respostas
- 1681 Exibições
- Última mensagem por LuizAquino

Seg Set 19, 2011 17:27
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] assintota vertical
por beel » Seg Set 05, 2011 12:58
- 2 Respostas
- 3462 Exibições
- Última mensagem por Jhonata

Dom Mai 27, 2012 00:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
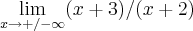
 ... isso quer dizer que não existem assintotas horizontais?
... isso quer dizer que não existem assintotas horizontais?
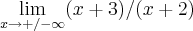
 ... isso quer dizer que não existem assintotas horizontais?
... isso quer dizer que não existem assintotas horizontais?

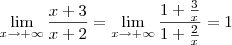
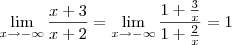
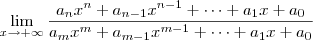
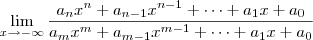
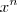 . Mas caso n < m, então você faz a divisão por
. Mas caso n < m, então você faz a divisão por 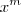 . Obviamente, se n = m tanta faz dividir por qualquer um deles.
. Obviamente, se n = m tanta faz dividir por qualquer um deles.
