Derivadas

por **Maykids** » Ter Mai 24, 2011 14:36

I ai pessoal tudo bom de novo?
entao eu nao consegui resolver mais uma leva de exercicios, hehe...
como eles possuem graficos eu recortei e fiz nos parametros pedidos, pelos adm...
nesse primeiro ele nao da "função" nem nada, e quer saber os valores da multiplicação entre as duas e depois a derivada.
Imagem

http://imageshack.us/photo/my-images/11/exercicio1.jpg/
http://imageshack.us/photo/my-images/11/exercicio1.jpg/

e esse aqui
nao sei nem começar, :S
desde ja obrigado ^^
Imagem

http://imageshack.us/photo/my-images/10/exercicio2.jpg/

por **LuizAquino** » Ter Mai 24, 2011 17:39

Maykids escreveu:como eles possuem gráficos eu recortei e fiz nos parâmetros pedidos, pelos adm...

A orientação é que seja escrito na mensagem todo o texto do exercício. Se por acaso o exercício tiver uma figura, então apenas a figura deve ser enviada como uma imagem. Vale lembrar (mais uma vez) que quando você envia o texto do exercício no formato de uma imagem, ele não é localizado pelas ferramentas de busca, o que é bastante prejudicial.

Além disso, procure aprender como inserir uma imagem diretamente em sua mensagem, para não ter que enviá-la para uma outra página. O processo é extremamente simples. Na edição de suas mensagens, basta usar a opção "Anexar arquivo".

Agora vejamos os exercícios.

Ao meu ver, o gráfico do primeiro exercício deveria ser algo como ilustra a figura abaixo. Vale destacar que para facilitar a dica que eu darei a seguir eu inseri também os ângulos $\alpha$ e $\beta$ .

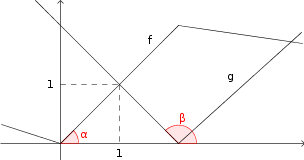
: exercício-derivada.png (4.28 KiB) Exibido 1885 vezes

Dica: Lembre-se que da interpretação geométrica sobre derivadas temos que $f^\prime(1) = \textrm{tg}\,\theta$ e $g^\prime(1) = \textrm{tg}\,\beta$ .

Já o segundo exercício podemos ilustrar com a figura abaixo. Você precisa demonstrar que não importando o ponto (c, f(c)) (com c > 0) que seja escolhido, a reta tangente ao gráfico de f nesse ponto irá determinar o triângulo COB que possui área de 2 unidades quadradas.

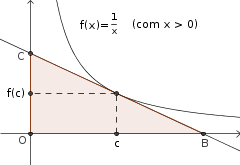
: exercício2-derivada.png (5.22 KiB) Exibido 1885 vezes

Dica: Lembre-se que a reta tangente ao gráfico de f no ponto (c, f(c)) é dada pela equação y - f(c) = f'(c)(x - c). Note que para calcular a área do triângulo você precisará determinar os pontos C e B nos quais a reta tangente intercepta os eixos.

por **Maykids** » Ter Mai 24, 2011 19:04

Professor eu olho olho, e nada escrevo e apago toda hora aqui, rs

se a f'(1) = tg $\alpha$
eu posso alegar que a tg $\alpha$ = 1?
eu acho que $\alpha$ = 45º
mais nao ta saindo nem uma ideia, em que posso fazer a multiplicação de duas funções sem as funções, e ainda calcular a derivada da resultante delas, :S

por **LuizAquino** » Ter Mai 24, 2011 19:14

Maykids escreveu:Professor eu olho olho, e nada escrevo e apago toda hora aqui, rs
se a f'(1) = tg $\alpha$
eu posso alegar que a tg $\alpha$ = 1?
eu acho que $\alpha = 45^\circ$

Esta alegação é falsa.

Maykids escreveu:mais nao ta saindo nem uma ideia, em que posso fazer a multiplicação de duas funções sem as funções, e ainda calcular a derivada da resultante delas, :S

Note que você não vai encontrar um valor numérico para as derivadas solicitadas no exercício. O que se pode fazer, considerando os dados do exercício, é determinar essas derivadas em função de $\alpha$ e $\beta$ .

por **Maykids** » Ter Mai 24, 2011 22:53

minha prova é amanha de manhã, :'( sera que so dessa vez vc nao pode me dar a resposta delas nao? por favor, =/
obrigado.att,

Derivadas

Derivadas

Derivadas

Re: Derivadas

Re: Derivadas

Re: Derivadas

Re: Derivadas

Quem está online