como determino as assíntotas verticais e horizontais dessa função:
f(x)= 4/x²-3x+2


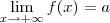 ou
ou 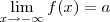 .
.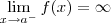 ou
ou 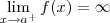 .
.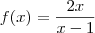 . Temos que:
. Temos que: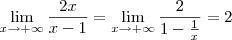 .
.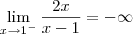 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes