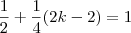O enunciado do exercício diz o seguinte:
Considere a variável aleatória X com a seguinte função de probabilidade:
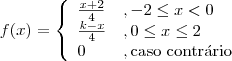
a) Determine, justificando detalhadamente, o valor da constante k.
Para que uma função seja uma
função de probabilidade ela deve ser sempre positiva e a integral em todo os seu domínio deve ser igual a 1.
O domínio dessa função é todo o conjunto dos números reais, então devemos ter:
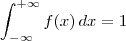
Note que essa função está definida em intervalos, de modo que fora do intervalo [-2, 2] ela é zero. Portanto, podemos simplificar essa integral para:
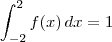
Por fim, a função tem uma expressão diferente para os intervalos [-2, 0) e [0, 2]. Portanto, temos que:
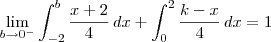
Note que esse limite que apareceu na primeira integral é só para dar conta do fato que em x=0 a função está definida como (k-x)/4 e não como (x+2)/4.
Resolvendo as integrais, obtemos:
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1](/latexrender/pictures/fe768a2ceb74b7a61b6b54c44f1af23d.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1](/latexrender/pictures/eddb21f7336363a3c1dec89adaadd9ac.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1](/latexrender/pictures/9719681947903a61d9d411e92f789825.png)
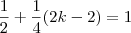

Sendo assim, para k=2 a integral em todo domínio de f será igual a 1. Além disso, note que para k=2 a função é sempre positiva.
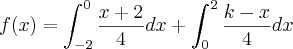

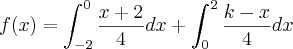


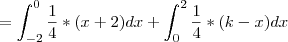



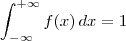
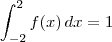
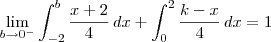
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1](/latexrender/pictures/fe768a2ceb74b7a61b6b54c44f1af23d.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1](/latexrender/pictures/eddb21f7336363a3c1dec89adaadd9ac.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1](/latexrender/pictures/9719681947903a61d9d411e92f789825.png)