 por Loretto » Dom Ago 22, 2010 16:05
por Loretto » Dom Ago 22, 2010 16:05
1) Estude a função f(x) = x^4-4x³ com relação aos intervalos de crescimento e decrescimento,com relação à concavidade e pontos de inflexão e esboce o gráfico de f.
Tentei achar a solução da seguinte forma :
1) Domínio : Reais
2) f'(x) = 4x³ - 12 x²
3) f''(x) = 12x² - 24x
4) Estudar ponto de crescimento e decrescimento :
12 x² - 24x = 0
![[*]delta[*] [*]delta[*]](/latexrender/pictures/f83ca5f5522df4607311528c877ba05e.png)
= 4
raízes = 2 e 0
4)
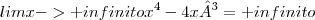
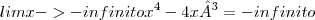
5) Os limites laterais não são necessários de serem calculados, pois a função é contínua em todos os pontos.
f(1) = -4
f(0) = 0
f(2) -32
f(-1) 5
Meu gráfico saiu errado, estou com dúvida pois a f(x) é de grau 4. Como faço esse exercício corretamente ? Obrigado !
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Esboçar o gráfico da função
por Carla Gomes » Seg Abr 01, 2013 14:47
- 0 Respostas
- 585 Exibições
- Última mensagem por Carla Gomes

Seg Abr 01, 2013 14:47
Funções
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7161 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Preciso da Resolução desse exercicio
por alexcaju » Sex Jan 17, 2014 19:58
- 0 Respostas
- 1074 Exibições
- Última mensagem por alexcaju

Sex Jan 17, 2014 19:58
Matemática Financeira
-
- Como resolvo problemas desse tipo?
por PriscilaMG » Dom Nov 22, 2009 12:25
- 1 Respostas
- 1908 Exibições
- Última mensagem por PriscilaMG

Dom Nov 22, 2009 12:33
Logaritmos
-
- Determine a medida h da altura desse triângulo...
por welton » Qui Out 23, 2014 14:44
- 1 Respostas
- 2621 Exibições
- Última mensagem por jcmatematica

Sex Out 24, 2014 22:11
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[*]delta[*] [*]delta[*]](/latexrender/pictures/f83ca5f5522df4607311528c877ba05e.png) = 4
= 4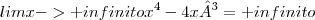
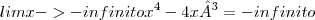



 .
.



