Prezados, bom dia!
Alguém poderia me ajudar como começo a resolver o problema abaixo? Eu sei que preciso usar derivada, mas não estou sabendo por onde começar uma vez que tem as constantes.
Um modelo para dispersão de um rumor é dado pela equação:
- equacao
- Capturar.PNG (2.46 KiB) Exibido 5561 vezes
onde p(t) é a proporção da população que já ouviu o boato no tempo t e a e k são constantes positivas.
(a) Quando a metade da população terá ouvido um rumor?
(b) Quando ocorre a maior taxa de dispersão do boato?
Obrigado!
,pois...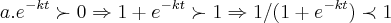
...para t=0,teremos q. ter pelo menos 2 pessoas p.dizer do rumor,logo:
...
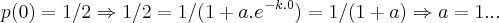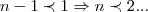logo,n é natural,o menor numero maior q. 2 é 3...logo,tomaremos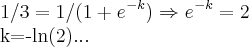
...
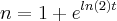,onde n e o numero de pessoas da populaçao que participa do rumor...
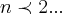ou memos p/
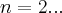,teriamos:
,ou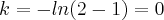 
,fato que nao resolveriamos o problema,pois 
...
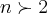,sendo n um natural,entao pelas condiçoes dadas do problema,nao havera soluçao...obrigado...
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.