Determine a equação da reta tangente ao gráfico da função a seguir nos pontos dados e trace o gráficos:
f(x) = -x² - 4 nos pontos P(1,3) e Q(0,4)
Achei o m(x) = lim -2x , mas não tô conseguindo traçar as retas no gráfico. Se fosse, por exemplo, em (X1 = 0), eu saberia.
/\x->0
Mas com esses pontos dados não sei como aplicar na fórmula y - f(X)= [m(X)][X - X1].
Obrigado!



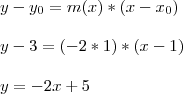
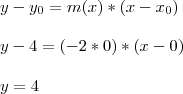


 .
.
 :
: