
É bastante fácil de resolver. Acontece que não sei porque motivo, no momento eu decidi retirar da integral o fator "-1" que multiplica o "s". Fazendo isso, no final estava obtendo uma resposta diferente, depois refiz sem retirar esse sinal e estava dando certo.
Resolvi então sair do problema que estava resolvendo pra tentar entender o que fiz de errado. Fiz os seguinte cálculos:
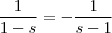
Integrando dos dois lados e somando as constantes em uma só:
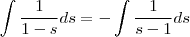
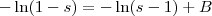
Multiplicando tudo por -1:

Ai está o problema. C é uma constante arbitrária. Se tomarmos C = 0 por exemplo, teríamos que:
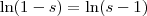
E isso não é possível.
O que fiz de errado aí? Se eu não seguir esse caminho de retirar o "-1" resolvo rápido e dá tudo certo. Mas queria entender o que aconteceu pra não cometer o erro em algum outro problema.


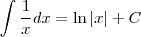
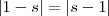
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.