 por fatalshootxd » Ter Mar 31, 2015 00:43
por fatalshootxd » Ter Mar 31, 2015 00:43
Eu tenho que resolver uma lista para estudar para uma prova porem ha 2 questoes que eu nao consigo fazer nem a pau.Eu ate chego em um resultado porem nao é o que esta no gabarito...que eu até estou achando que está errado...alguem me ajuda? tem que ser pra amanha.

-
fatalshootxd
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 31, 2015 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecanica
- Andamento: cursando
 por adauto martins » Sáb Abr 04, 2015 16:13
por adauto martins » Sáb Abr 04, 2015 16:13
para o calculo em coordenadas esfericas,temos:
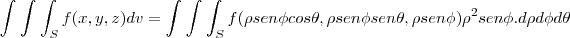
,onde
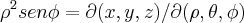
q. eh o jacobiano na mudança de variaveis...
entao...

,vamos encontrar o ponto de intersecçao dos solidos,ou seja o valor de
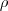
...
![\rho =\sqrt[]{3({x}^{2}+{y}^{2})}\Rightarrow {\rho}^{2}/3={x}^{2}+{y}^{2} \rho =\sqrt[]{3({x}^{2}+{y}^{2})}\Rightarrow {\rho}^{2}/3={x}^{2}+{y}^{2}](/latexrender/pictures/95c36d10979e4d3f1371bd382a31fbc3.png)
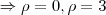
e
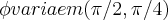
,pois o cone de revoluçao tem raios e altura iguais...logo
![\int_{0}^{3}{\rho}^{2}/{\rho}^{2}.\int_{\pi/2}^{\pi/4}sen\phi.\int_{0}^{2\pi}d\theta d\phi d\rho=\int_{0}^{3}}.\int_{\pi/2}^{\pi/4}sen\phi.2\pi.d\rho.d\phi=\int_{0}^{3}}(-(cos\pi/2-cos\pi/4).2\pi d\rho=4\pi.\sqrt[]{2}/2\int_{0}^{3}}d\rho=2.3.\sqrt[]{2}\pi=6.\sqrt[]{2}\pi \int_{0}^{3}{\rho}^{2}/{\rho}^{2}.\int_{\pi/2}^{\pi/4}sen\phi.\int_{0}^{2\pi}d\theta d\phi d\rho=\int_{0}^{3}}.\int_{\pi/2}^{\pi/4}sen\phi.2\pi.d\rho.d\phi=\int_{0}^{3}}(-(cos\pi/2-cos\pi/4).2\pi d\rho=4\pi.\sqrt[]{2}/2\int_{0}^{3}}d\rho=2.3.\sqrt[]{2}\pi=6.\sqrt[]{2}\pi](/latexrender/pictures/dd247862c54b336cac1c641757e3c102.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Coordenada Polar] Volume por Integral Dupla
por raimundoocjr » Qui Dez 12, 2013 19:42
- 0 Respostas
- 2404 Exibições
- Última mensagem por raimundoocjr

Qui Dez 12, 2013 19:42
Cálculo: Limites, Derivadas e Integrais
-
- Tripla Coordenada - Dúvida em resolução de tripla coordenada
por talesalberto » Sáb Nov 01, 2014 16:24
- 1 Respostas
- 1574 Exibições
- Última mensagem por adauto martins

Dom Nov 02, 2014 11:23
Álgebra Linear
-
- cálculo de integral
por jmario » Ter Mai 18, 2010 12:25
- 1 Respostas
- 3270 Exibições
- Última mensagem por MarcosFreitas

Qua Jun 02, 2010 13:04
Cálculo: Limites, Derivadas e Integrais
-
- CALCULO DE INTEGRAL
por Jaison Werner » Sex Jan 07, 2011 18:58
- 4 Respostas
- 3158 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 08, 2011 12:48
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Integral
por Nah23 » Ter Abr 26, 2011 13:30
- 1 Respostas
- 1829 Exibições
- Última mensagem por LuizAquino

Ter Abr 26, 2011 14:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





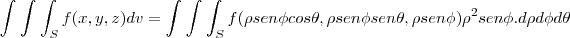 ,onde
,onde 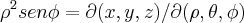 q. eh o jacobiano na mudança de variaveis...
q. eh o jacobiano na mudança de variaveis... ,vamos encontrar o ponto de intersecçao dos solidos,ou seja o valor de
,vamos encontrar o ponto de intersecçao dos solidos,ou seja o valor de 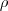 ...
...![\rho =\sqrt[]{3({x}^{2}+{y}^{2})}\Rightarrow {\rho}^{2}/3={x}^{2}+{y}^{2} \rho =\sqrt[]{3({x}^{2}+{y}^{2})}\Rightarrow {\rho}^{2}/3={x}^{2}+{y}^{2}](/latexrender/pictures/95c36d10979e4d3f1371bd382a31fbc3.png)
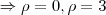 e
e 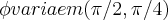 ,pois o cone de revoluçao tem raios e altura iguais...logo
,pois o cone de revoluçao tem raios e altura iguais...logo![\int_{0}^{3}{\rho}^{2}/{\rho}^{2}.\int_{\pi/2}^{\pi/4}sen\phi.\int_{0}^{2\pi}d\theta d\phi d\rho=\int_{0}^{3}}.\int_{\pi/2}^{\pi/4}sen\phi.2\pi.d\rho.d\phi=\int_{0}^{3}}(-(cos\pi/2-cos\pi/4).2\pi d\rho=4\pi.\sqrt[]{2}/2\int_{0}^{3}}d\rho=2.3.\sqrt[]{2}\pi=6.\sqrt[]{2}\pi \int_{0}^{3}{\rho}^{2}/{\rho}^{2}.\int_{\pi/2}^{\pi/4}sen\phi.\int_{0}^{2\pi}d\theta d\phi d\rho=\int_{0}^{3}}.\int_{\pi/2}^{\pi/4}sen\phi.2\pi.d\rho.d\phi=\int_{0}^{3}}(-(cos\pi/2-cos\pi/4).2\pi d\rho=4\pi.\sqrt[]{2}/2\int_{0}^{3}}d\rho=2.3.\sqrt[]{2}\pi=6.\sqrt[]{2}\pi](/latexrender/pictures/dd247862c54b336cac1c641757e3c102.png)


 .
.
 :
: