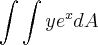, onde a região se localiza no primeiro quadrante e é limitada pelo círculo 
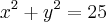.Bom, parece que é simples essa integral, mas infelizmente eu não consegui progredir o raciocínio. No começo até eu consegui reconhecer a região limitada, ou seja, o raio é 5 segundo a equação, e o intervalo do ângulo só pode estar entre 0 e
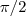, já que a região está no primeiro quadrante, até aí tudo bem. Na hora de converter para coordenadas polares, ficou assim: 
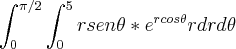, e na hora de integrar em relação a 
, deu 
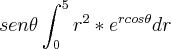pois o 
se comporta como uma constante para esse caso. Assim, caiu uma integral por partes , mas parece que não deu certo, pois na hora de chamar a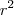 
de 
e derivar, vai ficar 
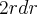o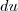 
, e muito menos integrar o 
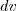. Será que tem outro método que simplifique isso, ou é inevitável? Enfim, se alguém puder me ajudar, eu agradeço desde já! 
Obrigado!
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.