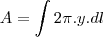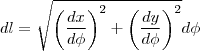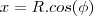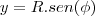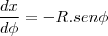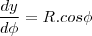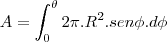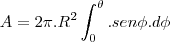por Francielly Novais » Sáb Mar 29, 2014 17:02
por Francielly Novais » Sáb Mar 29, 2014 17:02
- Considere uma superfície esférica de raio . Determine a área que é removida dessa superfície por um cone com vértice no centro da esfera, se, no vértice, a seção meridiana do cone tem um ângulo de 2? radianos.
Alguém poderia me ajudar nessa questão, seria de grande ajuda!
E um esboço feito:
http://sketchtoy.com/59910201 Eu fiz achando a equação do cone, agora estou na duvida. Eu acho a equação (área do cone) e integro ou tenho achar também a área da circunferência?
Quem seria a altura do cone.
O volume de um sólido por revolução é dado pela função V =??[f(x)]²dx
V= ?r²h
V= ?a²h
Quem seria h?
Me ajudem, n sei como resolver essa questão
-
Francielly Novais
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 29, 2014 16:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Dom Mar 30, 2014 12:18
por young_jedi » Dom Mar 30, 2014 12:18
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Volume de sólido de revolução
por VenomForm » Ter Abr 23, 2013 14:05
- 1 Respostas
- 1885 Exibições
- Última mensagem por young_jedi

Qua Abr 24, 2013 14:47
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Solido de Revolução
 por Amandarbastos » Qui Nov 30, 2017 18:37
por Amandarbastos » Qui Nov 30, 2017 18:37
- 0 Respostas
- 3886 Exibições
- Última mensagem por Amandarbastos

Qui Nov 30, 2017 18:37
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais Multiplas] Volume do solido
 por brunojorge29 » Ter Nov 27, 2012 01:55
por brunojorge29 » Ter Nov 27, 2012 01:55
- 2 Respostas
- 3914 Exibições
- Última mensagem por Guilherme Pimentel

Seg Jan 13, 2014 09:05
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Volume de um sólido obtido por rotação
 por Leon » Sex Dez 05, 2014 16:05
por Leon » Sex Dez 05, 2014 16:05
- 1 Respostas
- 3587 Exibições
- Última mensagem por Leon

Sex Dez 05, 2014 16:52
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais triplas] Calcular o centro de massa de um solido.
por amigao » Dom Mar 23, 2014 19:38
- 0 Respostas
- 1188 Exibições
- Última mensagem por amigao

Dom Mar 23, 2014 19:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.