 por fabriel » Qua Dez 11, 2013 16:40
por fabriel » Qua Dez 11, 2013 16:40
E ai pessoal, tudo trankuilo?
Então to estudando Equações diferenciais e não entendi uma passagem aqui, estou estudando a parte de variáveis separáveis.
Vejam só.
Notemos que equações do tipo:
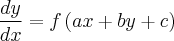
(1.1)
Onde a e b são constantes, não são equações de variáveis separáveis, mas podem ser reduzidas a elas por meio da seguinte substituição:
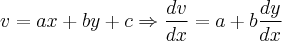
(1.2)
Substituindo em (1.1) temos:
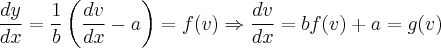
NÃO ENTENDI, o porque de concluir que
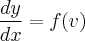
.
Eu agradeceria se alguém pudesse me ajudar.
Obrigado
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 17:24
por e8group » Qua Dez 11, 2013 17:24
fabriel escreveu:E ai pessoal, tudo trankuilo?
Então to estudando Equações diferenciais e não entendi uma passagem aqui, estou estudando a parte de variáveis separáveis.
Vejam só.
Notemos que equações do tipo:
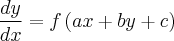
(1.1)
Onde a e b são constantes, não são equações de variáveis separáveis, mas podem ser reduzidas a elas por meio da seguinte substituição:
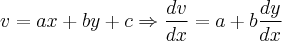
(1.2)
Substituindo em (1.1) temos:
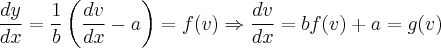
NÃO ENTENDI, o porque de concluir que
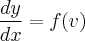
.
Eu agradeceria se alguém pudesse me ajudar.
Obrigado
A resposta para sua dúvida seria bem simples , pelo fato da substituição de variável feita . Não se é isso que você está com dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Qua Dez 11, 2013 18:48
por fabriel » Qua Dez 11, 2013 18:48
Sim, mas como que disso:
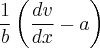
posso afirmar que é igual a isso
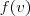
.
ou seja,
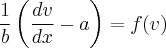
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 18:59
por e8group » Qua Dez 11, 2013 18:59
Sim . Segundo a mudança de variável
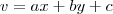
,teremos que
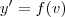
. Mas , derivando-se
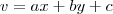
com respeito a

,vamos obter
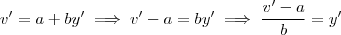
e assim
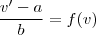
.
Bom não fiz nada de mais além da solução a qual você postou . Comente qualquer dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Qua Dez 11, 2013 19:14
por fabriel » Qua Dez 11, 2013 19:14
Tranquilo, estou me preucupando muito com Analise Matemática e estruturas algebricas... Tenso.. entendi, obrigado
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [EQUAÇÃO DIFERENCIAL] Forma separavel
por fabriel » Sáb Nov 02, 2013 12:40
- 1 Respostas
- 1979 Exibições
- Última mensagem por e8group

Sáb Nov 02, 2013 19:09
Cálculo: Limites, Derivadas e Integrais
-
- forma da equação
por Ana Maria da Silva » Sex Mar 08, 2019 09:31
- 0 Respostas
- 3296 Exibições
- Última mensagem por Ana Maria da Silva

Sex Mar 08, 2019 09:31
Equações
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12231 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3952 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2081 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
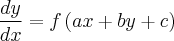 (1.1)
(1.1)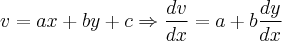 (1.2)
(1.2)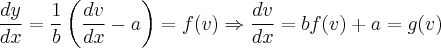
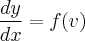 .
.


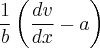 posso afirmar que é igual a isso
posso afirmar que é igual a isso 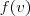 .
.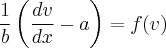
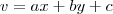 ,teremos que
,teremos que 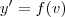 . Mas , derivando-se
. Mas , derivando-se  ,vamos obter
,vamos obter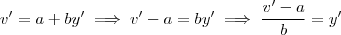 e assim
e assim 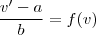 .
.  em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.