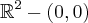por raimundoocjr » Ter Out 08, 2013 21:44
por raimundoocjr » Ter Out 08, 2013 21:44
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Q. 37 - Pág.: 811)
Determine o maior conjunto no qual a função é contínua.
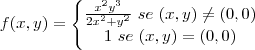
Como faço isso?
-
raimundoocjr
-
 por Bravim » Qui Out 10, 2013 00:58
por Bravim » Qui Out 10, 2013 00:58
Olha, para você fazer essa, você tem que calcular os limites iterados.
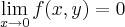
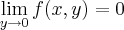
Bem, agora nós deveríamos verificar que os limites iterados obviamente dão zero. Neste caso, SE O LIMITE EXISTIR, ele deve ser igual a zero. Como em (0,0) o valor de
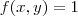
a função não será contínua em (0,0).Para todos os outros pontos do
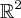
a função será contínua porque você tem uma divisão de polinômios e porque os limites iterados serão iguais.
Neste caso o maior conjunto que contém a função será:
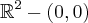
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Maior valor
por thadeu » Qua Nov 25, 2009 16:17
- 4 Respostas
- 2769 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:14
Álgebra Elementar
-
- Quem é maior?
por victoreis1 » Qui Nov 25, 2010 18:40
- 19 Respostas
- 16140 Exibições
- Última mensagem por MarceloFantini

Seg Dez 13, 2010 01:24
Desafios Fáceis
-
- maior fator primo
por Marcos Ivan » Sáb Ago 21, 2010 12:29
- 1 Respostas
- 2309 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 17:28
Geometria Analítica
-
- Maior valor da inequação
por maria cleide » Dom Mai 29, 2011 17:35
- 8 Respostas
- 4326 Exibições
- Última mensagem por maria cleide

Dom Jun 05, 2011 18:25
Sistemas de Equações
-
- derivada de ordem maior!
por giulioaltoe » Sex Jul 29, 2011 16:27
- 2 Respostas
- 1701 Exibições
- Última mensagem por giulioaltoe

Sex Jul 29, 2011 16:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
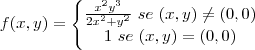

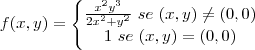
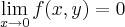
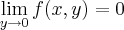
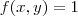 a função não será contínua em (0,0).Para todos os outros pontos do
a função não será contínua em (0,0).Para todos os outros pontos do 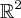 a função será contínua porque você tem uma divisão de polinômios e porque os limites iterados serão iguais.
a função será contínua porque você tem uma divisão de polinômios e porque os limites iterados serão iguais.