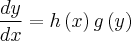
Mas não tenho total certeza sobre como tentar separar uma E.D.O corretamente.
Por exemplo, as equações a seguir eu resolvi por fator integrante mas acho que consigo separar. Consigo ou não ??
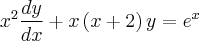
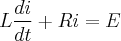
Onde
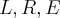 são constantes.
são constantes.Já nesta equação qual a diferença, em relação a separação, das formas abaixo:
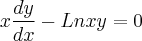
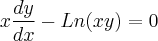


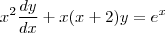
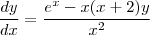
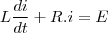
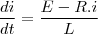
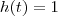 e
e 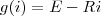
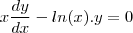
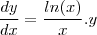
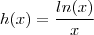 e
e 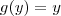
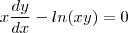
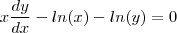
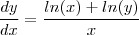
 e
e  ???
???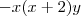
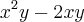
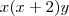
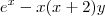
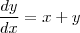
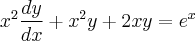
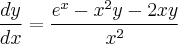
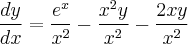
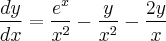
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)