


 de cada função do denominador e numerador após calcular seus limites . Observe que para
de cada função do denominador e numerador após calcular seus limites . Observe que para  vale a expressão que é equivalente a mesma postada:
vale a expressão que é equivalente a mesma postada: 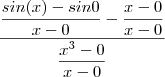 . Tomando o limite com
. Tomando o limite com 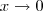 e utilizando suas regras operatórias , obtemos:
e utilizando suas regras operatórias , obtemos: 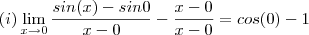 que devido a continuidade de
que devido a continuidade de 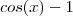 no ponto
no ponto  ,segue
,segue 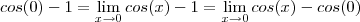 .
.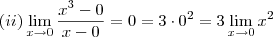 (Por quê ??)
(Por quê ??) 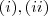 vemos que
vemos que 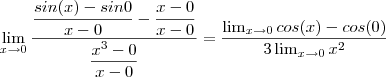 .Muliplicando o denominador e numerador por
.Muliplicando o denominador e numerador por  e seguindo o mesmo raciocínio utilizado nos itens acima , você obterá como resposta
e seguindo o mesmo raciocínio utilizado nos itens acima , você obterá como resposta 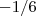 .
. 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.