estou com duvida na seguinte função na qual tenho que calcular o seu comprimento de arco:
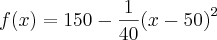;![\left[0,80 \right]](/latexrender/pictures/a3e6cc9c70053e4974b02e2c7d932721.png "\left[0,80 \right]")
sei que a formula para calcular o comprimento de um arco é:
![\int_{a}^{b}\sqrt[2]{{f'(x)}^{2}+1}dx](/latexrender/pictures/491b4c3bf37afa6052182900886a0bef.png "\int_{a}^{b}\sqrt[2]{{f'(x)}^{2}+1}dx")
então primeiro eu calculo a f'(x) que da:
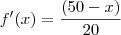
depois faço (f'(x))^2:
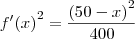
substituindo na formula:
![\int_{0}^{80}\sqrt[2]{\frac{{(50-x)}^{2}}{400}+1}dx](/latexrender/pictures/6fc436ebf82ba5f377f3962f4b35a415.png "\int_{0}^{80}\sqrt[2]{\frac{{(50-x)}^{2}}{400}+1}dx")
Agora vem minha duvida, devo primeiro fazer alguma substituição para continuar a integração?se sim qual?
agradeço desde já pela sua ajuda
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)