 por Henrique Bueno » Sex Abr 19, 2013 00:25
por Henrique Bueno » Sex Abr 19, 2013 00:25
Supondo que o lim f(x)=L quando x->p prove que existem r>0 e M>0 tais que
0<|x-p|<r => -M <=f(x)<=M
primeiramente ao analisar as afirmações, a primeira parte (0<|x-p|<r) é idêntica a definição de limite, somente empregou um r onde normalmente usamos um delta.
Usando que |f(x)-L|< E (onde E é aquele epslon eu acho, aquela letra grega)
-E < f(x)-L < E
-E -L < f(x) < E -L
embora eu tenha conseguido fazer uma sentença semelhante a -M <=f(x)<=M, não consigo definir um M através dela. Além disso acredito que era necessário relacionar o M e o r para que o limite fosse provado. Por favor, me ajudem !
-
Henrique Bueno
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 02, 2011 19:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sex Abr 19, 2013 02:00
por e8group » Sex Abr 19, 2013 02:00
Temos que
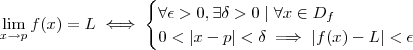
.
Como
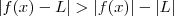
,
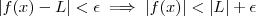
.
Tente concluir a parti daí .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 6105 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Prove a partir da definição de limite
por Ruan Petterson » Qui Nov 28, 2013 23:13
- 6 Respostas
- 3644 Exibições
- Última mensagem por e8group

Sex Nov 29, 2013 10:05
Cálculo: Limites, Derivadas e Integrais
-
- DERIVADA - cálculo através da definição
por emsbp » Sáb Abr 28, 2012 18:20
- 4 Respostas
- 1838 Exibições
- Última mensagem por emsbp

Qua Mai 02, 2012 06:41
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de limite através da série de MacLaurin
por Camargo » Qui Nov 25, 2010 15:13
- 0 Respostas
- 1903 Exibições
- Última mensagem por Camargo

Qui Nov 25, 2010 15:13
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Limites pela definiçao
 por JoaoLuiz07 » Qui Ago 27, 2015 16:55
por JoaoLuiz07 » Qui Ago 27, 2015 16:55
- 1 Respostas
- 1765 Exibições
- Última mensagem por adauto martins

Sáb Ago 29, 2015 20:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


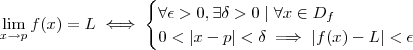 .
. 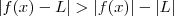 ,
, 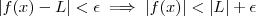 .
. 

 .
.



