 por brunnoguilherme » Dom Jan 13, 2013 00:32
por brunnoguilherme » Dom Jan 13, 2013 00:32
uma companhia possui trés fabricas produzindo o mesmo produto. se as fabricas A,B e C produzem x, y e z unidades respectivas, seus custos de fabricação são (3x²+200), (y²+400) e (2z²+300).
Se um pedido de 1.100 unidades dever ser entregue, use o método dos multiplicadores de lagrange para determinar como a produção dever ser distribuidora entre as trés fabricas, a fim de minimizar o custo total da fabricação.
-
brunnoguilherme
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jan 13, 2013 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Fisica
- Andamento: cursando
 por young_jedi » Dom Jan 13, 2013 12:52
por young_jedi » Dom Jan 13, 2013 12:52
primeiro voce tem que encontrar a equação do custo total
que nada mais é doque a soma dos custo de cada produto
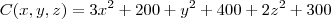
agora voce encontra a equação que relaciona as quantidades de cada produto
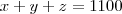
sendo assim voce tem uma função
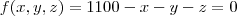
portanto voce pode encontrar uma função do tipo
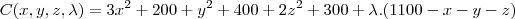
ai voce calcula as derivadas parciais e igula a zero
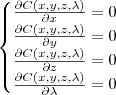
com isso voce vai ter um sistema de equações, é so resolver e encontrar os valores das incognitas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo - multiplicadores de Lagrange
por brunnoguilherme » Dom Jan 13, 2013 20:01
- 1 Respostas
- 1472 Exibições
- Última mensagem por timoteo

Dom Jan 13, 2013 23:07
Cálculo: Limites, Derivadas e Integrais
-
- Calculo - multiplicadores de Lagrange
por brunnoguilherme » Dom Jan 13, 2013 20:04
- 1 Respostas
- 1498 Exibições
- Última mensagem por Russman

Dom Jan 13, 2013 22:12
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de minimos,máximos usando multiplos de lagrange
por Fernandobertolaccini » Seg Jan 05, 2015 16:39
- 1 Respostas
- 1574 Exibições
- Última mensagem por Russman

Ter Jan 06, 2015 01:13
Cálculo: Limites, Derivadas e Integrais
-
- Multiplicadores de Lagrange
por Zkz » Sex Jun 05, 2009 21:00
- 0 Respostas
- 1899 Exibições
- Última mensagem por Zkz

Sex Jun 05, 2009 21:00
Cálculo: Limites, Derivadas e Integrais
-
- Multiplicadores de Lagrange
por luciamoura » Sex Nov 26, 2010 17:55
- 0 Respostas
- 1739 Exibições
- Última mensagem por luciamoura

Sex Nov 26, 2010 17:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


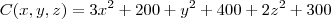
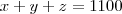
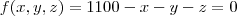
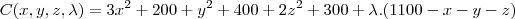
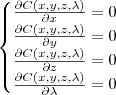

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.