- Pois bem, esta não é exatamente uma dúvida de um problema cuja resposta não consegui encontrar, mas sim uma curiosidade de minha pessoa. Meu professor lançou uma lista de exercícios de Regra da Cadeia e estou obcecado com um problema em particular, cuja resposta só consegui encontrar aplicando a Derivada do Produto mas não tive a mesma sorte aplicando a Derivada do Quociente. A questão é a seguinte:
Questão:
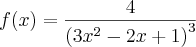
Tentativa pelo produto:
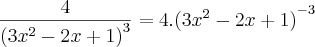

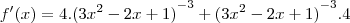
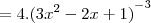
Para:
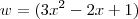
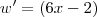
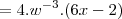
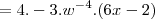
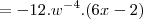
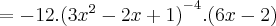

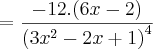
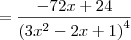 - O que bate com a resposta do Microsoft Mathematics.
- O que bate com a resposta do Microsoft Mathematics.Tentativa por Quociente
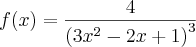
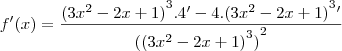
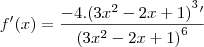
Para:
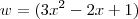
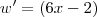
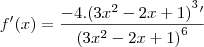
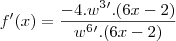
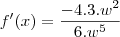
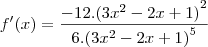
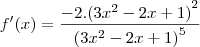
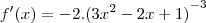
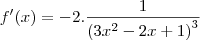
 - O que não bate nem com a resposta do Microsoft Mathematics, nem com a do gabarito.
- O que não bate nem com a resposta do Microsoft Mathematics, nem com a do gabarito.Gabarito
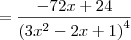 (Microsoft Mathematics) ou
(Microsoft Mathematics) ou![\frac{24(1-3x)}{4\sqrt[]{x}.\sqrt[]{4+3}.\sqrt[]{x}} \frac{24(1-3x)}{4\sqrt[]{x}.\sqrt[]{4+3}.\sqrt[]{x}}](/latexrender/pictures/e0edd6ef95ba1061f726eb7f7193882c.png) (Professor)
(Professor)---------------------------------------------------------------------------------------------
Obrigado, desde já, pela atenção que sempre retribuem neste fórum. Abraços.
Ass: Matheus L. Oliveira.


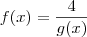 .
.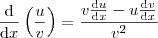
 e
e 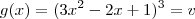 , temos:
, temos: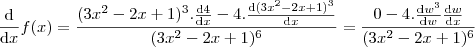
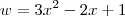 para aplicar a regra da cadeia e o zero que surge vem de
para aplicar a regra da cadeia e o zero que surge vem de 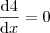 .
.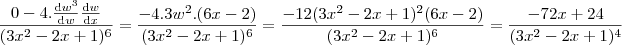
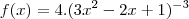 e como
e como 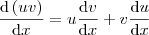 então tomando
então tomando 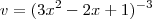 temos:
temos: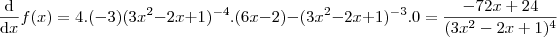
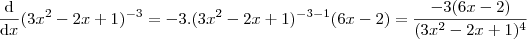 .
.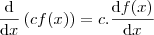 , isto é, "a constante sai fora da derivada"!. Tente fazer assim e veja se chega no mesmo resultado!
, isto é, "a constante sai fora da derivada"!. Tente fazer assim e veja se chega no mesmo resultado!

 .
.



