um lado do retangulo mede x sendo este a base e tabem o diametro do semi-circulo, o outro ladó mede y
sendo assim a soma dos lados do retangulo com o semi-circulo sera dada pelo perimetro p
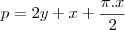
da onde tiramos
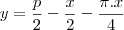
agora calculando as areas do retangulo e do semi-circulo

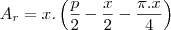
e a do semi-circulo
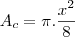
vamos admitir que no semi-circrulo a quantidade de luz permitida seja q e no retangulo seja 2q, então a quantidade de luz total sera
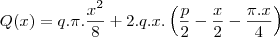
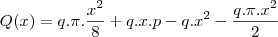
para encontrar seu valor de maximo derivamos com relação a x e igualamos a zero
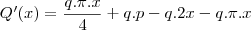
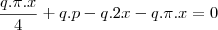
como tudo esta multiplicado por q podemos simplificar
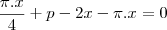
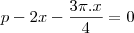
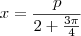
este é o valor de x agora voce tem que encontra y



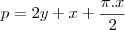
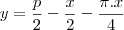

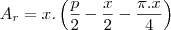
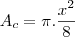
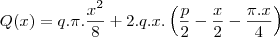
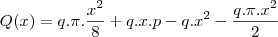
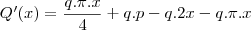
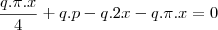
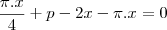
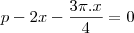
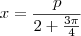




 .
.
 :
: