Olá LUCKYSB. Para resolver esse problema eu vou contar com a sua visão da figura em 3 dimensões, pois eu só vou postar os desenhos necessários para explicar os apótemas. Então vamos lá:
Primeiramente vamos a algumas considerações:

= aresta menor do tronco
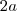
= aresta maior do tronco

= altura
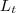
= apótema do tronco
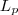
= apótema da pirâmide
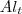
= área lateral do tronco
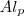
= área lateral da pirâmide
Para resolver o problema basta exprimirmos as áreas laterais em função de
a e
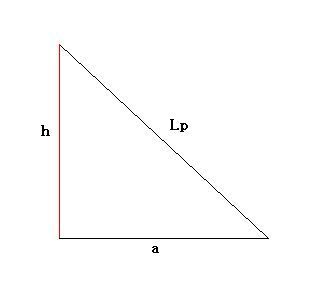
h. Comecemos com a área lateral do tronco:
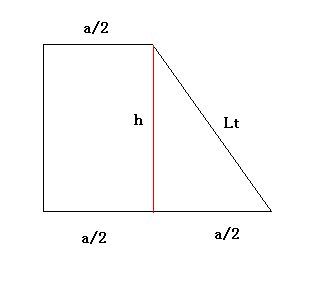
- apótema tronco.jpg (6.13 KiB) Exibido 3441 vezes
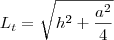
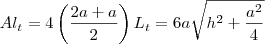
Para a pirâmide:
- apótema pirâmide.jpg (5.08 KiB) Exibido 3441 vezes
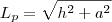
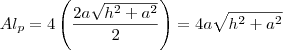
Igualando as duas áreas:
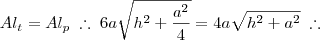
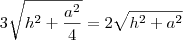
Elevamos ambos os membros ao quadrado:
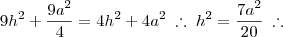
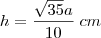
Até a próxima.
Editado pela última vez por
Douglasm em Qua Jun 02, 2010 22:09, em um total de 2 vezes.



 = aresta menor do tronco
= aresta menor do tronco 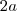 = aresta maior do tronco
= aresta maior do tronco  = altura
= altura 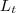 = apótema do tronco
= apótema do tronco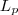 = apótema da pirâmide
= apótema da pirâmide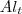 = área lateral do tronco
= área lateral do tronco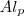 = área lateral da pirâmide
= área lateral da pirâmide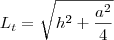
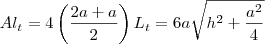
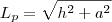
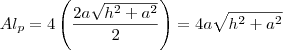
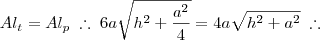
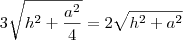
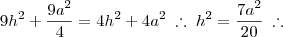
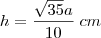


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)