 por Douglasm » Seg Mai 24, 2010 13:08
por Douglasm » Seg Mai 24, 2010 13:08
Olá jmario. Derivadas parciais consistem em derivar a equação em relação a uma variável, enquanto mantém as outras constantes. Farei a primeira para que você veja como é, e depois sugiro que tente você mesmo fazer as demais.
![f(x,y) = sen \left(\frac{x}{1+y}\right) \; \therefore \; \frac{\partial \left[sen \left(\frac{x}{1+y}\right)\right]}{\partial x} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{1}{1+y} f(x,y) = sen \left(\frac{x}{1+y}\right) \; \therefore \; \frac{\partial \left[sen \left(\frac{x}{1+y}\right)\right]}{\partial x} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{1}{1+y}](/latexrender/pictures/fe6284eedc4b9d6ad5cf3623de5ab1c0.png)
Aqui, tudo o que foi feito foi derivar a função, apenas em relação a variável
x, considerando
y como constante. Processo análogo é usado para resolver as outras. Caso ainda persista a dúvida, poste aqui.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Ter Mai 25, 2010 09:30
por jmario » Ter Mai 25, 2010 09:30
Oi Douglas
Não daria para você resolver todas as derivadas para eu tentar entender, porque eu não entendi.
Não era para ficar só

porque tem que multiplicar

Não entendi porque tem que multiplicar.
E tem também a segunda função para derivar, vc não poderia resolver pra mim?
Agradeço muito
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Ter Mai 25, 2010 12:19
por jmario » Ter Mai 25, 2010 12:19
Eu não entendi a derivada de
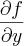
porque virou
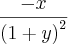
não está derivando em relação o y, assim não era para ficar
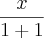
Me desculpe, mas não entendi de novo
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Ter Mai 25, 2010 13:00
por jmario » Ter Mai 25, 2010 13:00
Eu entendi tudo, só não entendi o começo
porque
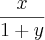
vira
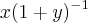
o x não era para ser constante
Não entendi essa derivada
Me ajude a entender
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10891 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13196 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14802 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5116 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
















![f(x,y) = sen \left(\frac{x}{1+y}\right) \; \therefore \; \frac{\partial \left[sen \left(\frac{x}{1+y}\right)\right]}{\partial x} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{1}{1+y} f(x,y) = sen \left(\frac{x}{1+y}\right) \; \therefore \; \frac{\partial \left[sen \left(\frac{x}{1+y}\right)\right]}{\partial x} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{1}{1+y}](/latexrender/pictures/fe6284eedc4b9d6ad5cf3623de5ab1c0.png)







![\frac{\partial f}{\partial y} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{-x}{(1+y)^2} \frac{\partial f}{\partial y} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{-x}{(1+y)^2}](/latexrender/pictures/ba5f9d05fa5ddfcb49a66afae2971167.png)




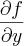
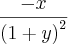
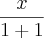


![\frac{\partial \left[\frac{x}{1+y}\right]}{\partial y} = \frac{\partial \left[x . (1+y)^{-1}\right]}{\partial y} = \frac{\partial \left[\frac{x}{1+y}\right]}{\partial y} = \frac{\partial \left[x . (1+y)^{-1}\right]}{\partial y} =](/latexrender/pictures/d5c9767d3bca2e5977e38dbe1bf31d0e.png)


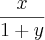 vira
vira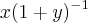


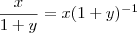

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.