Limites com 2 variáveis

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Limites com 2 variáveis

Regras do fórum
Responder

Limites com 2 variáveis

Mensagempor rstoque » Seg Jun 04, 2018 17:29

Estou com uma dúvida a respeito da resolução deste limite, pois quando eu tento resolvê-lo eu me confundo na hora de utilizar produtos notáveis no numerador.

\lim_{(x,y) \rightarrow \ (1,1)}{\frac{(x-1)^{4/3}-(y-1)^{4/3}}{(x-1)^{2/3}+(y-1)^{2/3}}}

Eu poderia desmembrar o numerador desta função assim...
\frac{(x-1)^{2/3}-(y-1)^{2/3}\cdot (x-1)^{2/3}+(y-1)^{2/3}}{(x-1)^{2/3}+(y-1)^{2/3}} ???

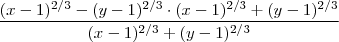
estou agarrado nessa resolução porque não estou concordando com ela, mas ao mesmo tempo ela faz sentido aff

desde já agradeço pessoal, abraços
rstoque
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Seg Jun 04, 2018 17:17
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Civil
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

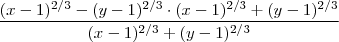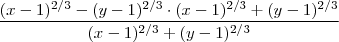Índice do fórum