4) Considerando a função y = lnx e a equação diferencial ordinária x.y’’ + y’ = 0, pode-se afirmar que
:
A.( ) y = lnx é uma solução para a EDO dada no intervalo I = [0, +infinito ).
B.( ) y = lnx é uma solução para a EDO dada no intervalo I = [0, + infinito].
C.( ) y = lnx é uma solução para a EDO dada no intervalo I = [0, + infinito).
D.( ) y = lnx é uma solução para a EDO dada no intervalo I = [– 1, + ).
Pelas minhas contas, deveria ser I = (0,+infinito). com PARENTESES no inicio e no fim, vi que a alternativa A e C, são iguais, será que estou certo? em uma delas deveria ser parenteses no inicio e fim?
onde está escrito +infinito é pq nao consegui por o simbolo.
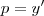,teremos entao: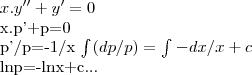
![x.y''+y'=0
x.p'+p=0
p'/p=-1/x
\int_{}^{}(dp/p)=\int_{}^{}-dx/x+c
[tex]y'={e}^{-lnx+c}={e}^{c}.{e}^{-lnx}=k/x...
\int_{}^{}y'=k.\int_{}^{}dx/x+c
y=k.lnx+c...k,c \in \Re...](/latexrender/pictures/625a2ad4b95a00d5d300168539fc834b.png "x.y''+y'=0
x.p'+p=0
p'/p=-1/x
\int_{}^{}(dp/p)=\int_{}^{}-dx/x+c
[tex]y'={e}^{-lnx+c}={e}^{c}.{e}^{-lnx}=k/x...
\int_{}^{}y'=k.\int_{}^{}dx/x+c
y=k.lnx+c...k,c \in \Re...")
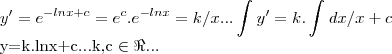
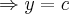,logo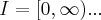
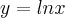é uma soluçao da equaçao dif. dada,pois o espaço-soluçao,ou famila de curvas é:
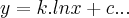,bom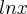 
,nao é definida em 
,pois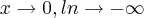 
,logo o espaço-soluçao esta definido no 
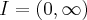,como vc propos e nao esta nas alternativas,acho precisa buscar um outro livro-texto...![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)