Como provar os seguintes limites pela definição?
a) Lim (x² - 2x + 1) = 1
x->2
b) lim (x² + 4x + 4) = 1
x->-1
c) lim (3x² - 7x +2) = -2
x->1



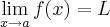
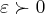 ,existe pelo menos um
,existe pelo menos um 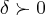 (existem ifinitos deltas,por que?),tal que satisfaça a:
(existem ifinitos deltas,por que?),tal que satisfaça a: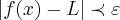 ...entao vamos a questao a),as outras ficam como exercicios...
...entao vamos a questao a),as outras ficam como exercicios... :
: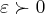 ,existe pelo um
,existe pelo um 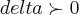 ,
,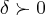 ...esse
...esse  tera q. ser em funçao do
tera q. ser em funçao do  dado,ou seja:
dado,ou seja: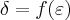 e geralmente,escolhe-se o menor
e geralmente,escolhe-se o menor  ,ou seja
,ou seja ![\delta =min[{\delta}_{1},{\delta}_{2},...] \delta =min[{\delta}_{1},{\delta}_{2},...]](/latexrender/pictures/d4247bbef86a62e625a9a6c176f73ffc.png) ...agora vamos ao calculo...temos q.
...agora vamos ao calculo...temos q.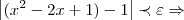 e q.
e q.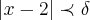
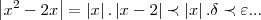 ,como
,como 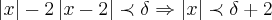 ,logo temos q.
,logo temos q.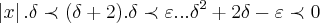 ...resolvendo essa inequaçao,encontraremos dois deltas...
...resolvendo essa inequaçao,encontraremos dois deltas...![{\delta}_{1}=\sqrt[]{1+\varepsilon}-1,{\delta}_{2}=\sqrt[]{1+\varepsilon}+1... {\delta}_{1}=\sqrt[]{1+\varepsilon}-1,{\delta}_{2}=\sqrt[]{1+\varepsilon}+1...](/latexrender/pictures/3ab1e8b9e36a928ae2654c9f0fc5400a.png) ...vamos tomar
...vamos tomar 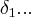 ...logo,teremos:
...logo,teremos:![\left|({x}^{2}-2x+1)-1 \right|=\left|{x}^{2}-2x \right|\preceq\left|x \right|.\left|x-2 \right|\prec (\delta+2).\delta={\delta}^{2}+2.\delta={(\sqrt[]{\varepsilon+1}-1})^{2}+2.(\sqrt[]{\varepsilon+1})=...\prec \varepsilon \left|({x}^{2}-2x+1)-1 \right|=\left|{x}^{2}-2x \right|\preceq\left|x \right|.\left|x-2 \right|\prec (\delta+2).\delta={\delta}^{2}+2.\delta={(\sqrt[]{\varepsilon+1}-1})^{2}+2.(\sqrt[]{\varepsilon+1})=...\prec \varepsilon](/latexrender/pictures/244cca570e64f5ff9db7f6639bd3d9fb.png) ...
...
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)