 por b11adriano » Sáb Out 18, 2014 18:47
por b11adriano » Sáb Out 18, 2014 18:47
O fator integrante da função,
dy/dx -2yx=x é dada por:
-
b11adriano
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Out 04, 2014 14:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: egenharia de produçao
- Andamento: cursando
 por adauto martins » Dom Out 19, 2014 14:28
por adauto martins » Dom Out 19, 2014 14:28
fator integrante de uma EDO e uma funçao
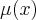
tal q.
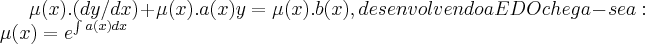
...logo
a EDO apresentada:dy/dx-2xy=x...
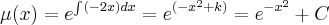
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações diferenciais] Fator integrante
por brunojorge29 » Qua Jun 19, 2013 10:52
- 2 Respostas
- 1216 Exibições
- Última mensagem por adauto martins

Ter Out 21, 2014 18:50
Cálculo: Limites, Derivadas e Integrais
-
- maior fator primo
por Marcos Ivan » Sáb Ago 21, 2010 12:29
- 1 Respostas
- 2408 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 17:28
Geometria Analítica
-
- /fATOR COMUM EM EVIDENCIA ME AJUDEM !!!!
por Reidson » Dom Ago 04, 2013 23:56
- 1 Respostas
- 1318 Exibições
- Última mensagem por Russman

Seg Ago 05, 2013 07:36
Álgebra Elementar
-
- [Integral Definida] Denominador c/ fator x e raiz de binômio
por Matheus Lacombe O » Dom Mar 17, 2013 17:35
- 2 Respostas
- 5913 Exibições
- Última mensagem por Matheus Lacombe O

Qua Mar 20, 2013 13:25
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração - multiplicando pelo fator unitário
por Victor Mello » Qui Nov 21, 2013 18:37
- 2 Respostas
- 1715 Exibições
- Última mensagem por Victor Mello

Qui Nov 21, 2013 23:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



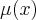 tal q.
tal q.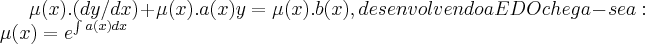 ...logo
...logo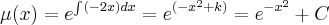 ...
...