 por LukasTsunami » Qui Out 09, 2014 14:58
por LukasTsunami » Qui Out 09, 2014 14:58
Seguinte, estou com uma dúvida tremenda, porque não consigo entender uma questão. Já fiz ela de várias formas, seja por propriedades dos limites, dividindo um limite pra cada termo, sendo multiplicando ambos os termos e depois continuando, mas mesmo assim não consigo resolver esse limite seguindo a regra (unica que me passaram no momento)
lim x -> 0 de (Senx)/x = 1...
a conta é a seguinte:
lim x -> 0 de [(x * cos3x) / cos2x]
De todas as formas que faço, a resposta dá Zero. Porém no livro, a resposta está 1/2. Não consegui achar resolução pro cálculo acima dar 1/2 de forma alguma e do porquê disso... O enunciado dá calcule, e depois os limites...
Uma pergunta... num limite trigonométrico, a resposta pode ser zero?
Vide anexo a conta montada certinho:
E depois a forma que EU pensei na conta... (uma delas), obrigado
- Anexos
-
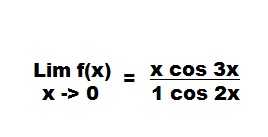
- limite.jpg (7.93 KiB) Exibido 978 vezes
-

-
LukasTsunami
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Out 09, 2014 14:39
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por adauto martins » Sáb Out 11, 2014 14:29
por adauto martins » Sáb Out 11, 2014 14:29
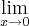
A=
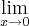
x.(cos(3x)/cos(2x))=
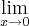
x.(cos(2x+x)/cos(2x))=
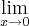
(cos(2x).cos(x)-sen(2x)sen(x)/2.cos(x).(sen(x)/x)),como
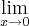
sex/x=1,temos:
A=1/2...pois,
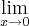
(cos2x.cosx=1,
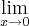
sen2x.sex=0 e
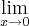
cosx=1...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 4853 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7040 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] calculo de limite trigonométrico
por PRADO » Dom Mai 22, 2016 17:01
- 2 Respostas
- 5459 Exibições
- Última mensagem por PRADO

Sex Jun 03, 2016 23:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico]
por Ana_Rodrigues » Qui Jan 26, 2012 18:54
- 4 Respostas
- 2718 Exibições
- Última mensagem por Ana_Rodrigues

Sex Jan 27, 2012 14:28
Cálculo: Limites, Derivadas e Integrais
-
- Limite trigonométrico
por jmoura » Dom Mar 25, 2012 21:25
- 2 Respostas
- 1985 Exibições
- Última mensagem por LuizAquino

Seg Mar 26, 2012 13:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


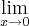 A=
A=

 .
.



