 por RonnieAlmeida » Qui Mai 22, 2014 16:58
por RonnieAlmeida » Qui Mai 22, 2014 16:58
Uma partícula move-se ao longo da curva
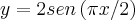
. Quando a partícula passa pelo ponto
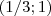
, sua coordenada

cresce a uma taxa de
![\sqrt[2]{10} cm/s \sqrt[2]{10} cm/s](/latexrender/pictures/c793b56faa9fe37964bf745abaad2a12.png)
. Quão rápido a distância da partícula à sua origem está variando nesse momento ?
-
RonnieAlmeida
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mai 22, 2014 16:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por alienante » Dom Jun 15, 2014 07:59
por alienante » Dom Jun 15, 2014 07:59
Olha a taxa de variação do deslocamento é
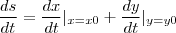
.Como
![\frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=\sqrt[]{10}cm/s\,\Rightarrow\,\frac{dy}{dt}{| \right|}_{y=1}=2cos\left(\frac{\pi x}{2} \right)\frac{\pi}{2}\frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=2cos(\frac{\pi}{6})\frac{\pi}{2}\cdot\sqrt[]{10}=\frac{\sqrt[]{30}\pi}{2}cm/s\,\Rightarrow\,\frac{ds}{dt}=\sqrt[]{10}+\frac{\sqrt[]{30}\pi}{2}=\frac{\sqrt[]{10}\left(2+\pi\sqrt[]{3} \right)}{2}cm/s \frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=\sqrt[]{10}cm/s\,\Rightarrow\,\frac{dy}{dt}{| \right|}_{y=1}=2cos\left(\frac{\pi x}{2} \right)\frac{\pi}{2}\frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=2cos(\frac{\pi}{6})\frac{\pi}{2}\cdot\sqrt[]{10}=\frac{\sqrt[]{30}\pi}{2}cm/s\,\Rightarrow\,\frac{ds}{dt}=\sqrt[]{10}+\frac{\sqrt[]{30}\pi}{2}=\frac{\sqrt[]{10}\left(2+\pi\sqrt[]{3} \right)}{2}cm/s](/latexrender/pictures/de1162da70b516dcff828ba87b020012.png)
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Taxas Relacionadas]
por Ana_Rodrigues » Seg Nov 14, 2011 10:02
- 2 Respostas
- 4593 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 12:19
Cálculo: Limites, Derivadas e Integrais
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:48
- 0 Respostas
- 1466 Exibições
- Última mensagem por RonnieAlmeida

Qui Mai 22, 2014 16:48
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Lorijuca » Qui Mai 29, 2014 22:23
- 0 Respostas
- 2956 Exibições
- Última mensagem por Lorijuca

Qui Mai 29, 2014 22:23
Cálculo: Limites, Derivadas e Integrais
-
- TAXAS RELACIONADAS
por Daniela[ » Sáb Jul 05, 2014 15:15
- 3 Respostas
- 6977 Exibições
- Última mensagem por young_jedi

Dom Jul 06, 2014 14:25
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Fernandobertolaccini » Sáb Out 25, 2014 09:57
- 5 Respostas
- 4579 Exibições
- Última mensagem por Fernandobertolaccini

Sáb Out 25, 2014 12:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
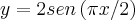 . Quando a partícula passa pelo ponto
. Quando a partícula passa pelo ponto 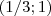 , sua coordenada
, sua coordenada  cresce a uma taxa de
cresce a uma taxa de ![\sqrt[2]{10} cm/s \sqrt[2]{10} cm/s](/latexrender/pictures/c793b56faa9fe37964bf745abaad2a12.png) . Quão rápido a distância da partícula à sua origem está variando nesse momento ?
. Quão rápido a distância da partícula à sua origem está variando nesse momento ?
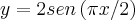 . Quando a partícula passa pelo ponto
. Quando a partícula passa pelo ponto 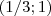 , sua coordenada
, sua coordenada  cresce a uma taxa de
cresce a uma taxa de ![\sqrt[2]{10} cm/s \sqrt[2]{10} cm/s](/latexrender/pictures/c793b56faa9fe37964bf745abaad2a12.png) . Quão rápido a distância da partícula à sua origem está variando nesse momento ?
. Quão rápido a distância da partícula à sua origem está variando nesse momento ?
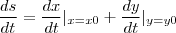 .Como
.Como![\frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=\sqrt[]{10}cm/s\,\Rightarrow\,\frac{dy}{dt}{| \right|}_{y=1}=2cos\left(\frac{\pi x}{2} \right)\frac{\pi}{2}\frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=2cos(\frac{\pi}{6})\frac{\pi}{2}\cdot\sqrt[]{10}=\frac{\sqrt[]{30}\pi}{2}cm/s\,\Rightarrow\,\frac{ds}{dt}=\sqrt[]{10}+\frac{\sqrt[]{30}\pi}{2}=\frac{\sqrt[]{10}\left(2+\pi\sqrt[]{3} \right)}{2}cm/s \frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=\sqrt[]{10}cm/s\,\Rightarrow\,\frac{dy}{dt}{| \right|}_{y=1}=2cos\left(\frac{\pi x}{2} \right)\frac{\pi}{2}\frac{dx}{dt}{| \right|}_{x=\frac{1}{3}}=2cos(\frac{\pi}{6})\frac{\pi}{2}\cdot\sqrt[]{10}=\frac{\sqrt[]{30}\pi}{2}cm/s\,\Rightarrow\,\frac{ds}{dt}=\sqrt[]{10}+\frac{\sqrt[]{30}\pi}{2}=\frac{\sqrt[]{10}\left(2+\pi\sqrt[]{3} \right)}{2}cm/s](/latexrender/pictures/de1162da70b516dcff828ba87b020012.png)


 .
.



