luisbaixo escreveu:Faça a expansão da função f(x) = x , 0<x<2 em uma série de fourier e senos e outra de cossenos.
Como você deve entender, se

é uma
função par contínua no intervalo
![[-a,a] [-a,a]](/latexrender/pictures/188b8d2ccb3b1d52985a3a3e5cf71fdb.png)
então o respectivo Coeficiente de Fourier associado a senos dessa função é nulo:
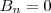
. Mas, se

é uma
função ímpar contínua no intervalo
![[-a,a] [-a,a]](/latexrender/pictures/188b8d2ccb3b1d52985a3a3e5cf71fdb.png)
então o respectivo Coeficiente de Fourier associado a cossenos dessa função é nulo:
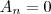
.
Já que a função

está definida somente para o intervalo
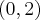
, isto é, não há nenhuma informação ou indício de que a mesma é periódica, nós podemos tomar uma extensão periódica desta função que, em geral, chama-se
prolongamento par ou
prolongamento ímpar para que seja possível a expansão da mesma em Série de Fourier. Lembre-se que esta expansão somente é válida para funções periódicas!!
Portanto, faça

ser ímpar, periódica no intervalo
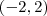
e expanda em Série de Fourier. A Série terá somente termos em senos e, então, podemos chama-la de Série de Fourier de Senos. Agora repita o mesmo procedimento , porém com a função sendo par! A Série terá somente termos em cossenos e, então, podemos chama-la de Série de Fourier de Cossenos.
Sim, a mesma função definida para o intervalo
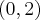
terá duas formas diferentes de representação. Fantástico, não?
(:


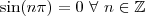 .
.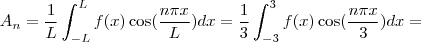
![=\frac{1}{3}\int_{-3}^{3}f(x)\cos(\frac{n \pi x}{3})dx = \frac{1}{3}\left [ \int_{-3}^{0}-x\cos(\frac{n \pi x}{3})dx + \int_{0}^{3}x\cos(\frac{n \pi x}{3})dx\right ]= =\frac{1}{3}\int_{-3}^{3}f(x)\cos(\frac{n \pi x}{3})dx = \frac{1}{3}\left [ \int_{-3}^{0}-x\cos(\frac{n \pi x}{3})dx + \int_{0}^{3}x\cos(\frac{n \pi x}{3})dx\right ]=](/latexrender/pictures/e70180fe2007eb28dc3a265e277c06cc.png)
![=\frac{1}{3}\left [ \frac{18}{\pi^2n^2} (\pi n \sin(\pi n)+\cos(\pi n)-1) \right ] =\frac{1}{3}\left [ \frac{18}{\pi^2n^2} (\pi n \sin(\pi n)+\cos(\pi n)-1) \right ]](/latexrender/pictures/023ebdb5814eebd77c815b14cc3e10d6.png)
 , temos
, temos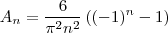
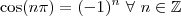 . Verifique q é verdade!!
. Verifique q é verdade!!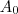 eu concordo com você. Daí, a série vai ser
eu concordo com você. Daí, a série vai ser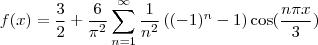
 , um
, um 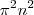 e o
e o  era
era  .Detalhes. A parte grossa(definir limites de integração, particionar o intervalo, efetuar as integrações) eu acredito que você tenha feito certo!
.Detalhes. A parte grossa(definir limites de integração, particionar o intervalo, efetuar as integrações) eu acredito que você tenha feito certo!
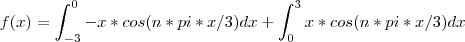
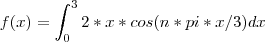 , dai eu acho que devo ter feito algo errado por isso que acho que ficou 12 ao invés de 6 hehe , talvez tenha errado na integração por partes também pra faltar o n²pi² , mas na prova resolverei com mais calma haha
, dai eu acho que devo ter feito algo errado por isso que acho que ficou 12 ao invés de 6 hehe , talvez tenha errado na integração por partes também pra faltar o n²pi² , mas na prova resolverei com mais calma haha é uma
é uma ![[-a,a] [-a,a]](/latexrender/pictures/188b8d2ccb3b1d52985a3a3e5cf71fdb.png) , então
, então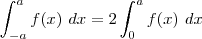 .
.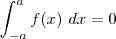
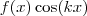 e
e  você pode estudar a paridade desse produto de funções e aplicar diretamente na integral. Uma função par multiplicada por uma outra função par, é par. E uma função par multiplicada por uma função ímpar, é ímpar. Assim, o coeficiente que envolve seno e uma função ímpar será sempre nulo. Como é o caso da sua função:
você pode estudar a paridade desse produto de funções e aplicar diretamente na integral. Uma função par multiplicada por uma outra função par, é par. E uma função par multiplicada por uma função ímpar, é ímpar. Assim, o coeficiente que envolve seno e uma função ímpar será sempre nulo. Como é o caso da sua função: 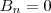 .
.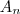 você pode tomar, já que
você pode tomar, já que 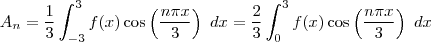
![[0,3] [0,3]](/latexrender/pictures/ed9c05fe24c0f49f5d73f494a921e0c4.png) temos
temos  , então
, então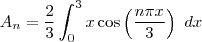
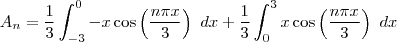
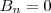 . Mas, se
. Mas, se 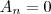 .
.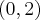 , isto é, não há nenhuma informação ou indício de que a mesma é periódica, nós podemos tomar uma extensão periódica desta função que, em geral, chama-se
, isto é, não há nenhuma informação ou indício de que a mesma é periódica, nós podemos tomar uma extensão periódica desta função que, em geral, chama-se 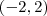 e expanda em Série de Fourier. A Série terá somente termos em senos e, então, podemos chama-la de Série de Fourier de Senos. Agora repita o mesmo procedimento , porém com a função sendo par! A Série terá somente termos em cossenos e, então, podemos chama-la de Série de Fourier de Cossenos.
e expanda em Série de Fourier. A Série terá somente termos em senos e, então, podemos chama-la de Série de Fourier de Senos. Agora repita o mesmo procedimento , porém com a função sendo par! A Série terá somente termos em cossenos e, então, podemos chama-la de Série de Fourier de Cossenos. 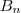 que devia ser nulo. :/
que devia ser nulo. :/