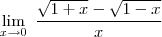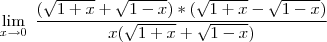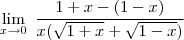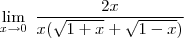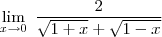por Rafael Zanelato » Seg Mar 31, 2014 14:17
por Rafael Zanelato » Seg Mar 31, 2014 14:17
Estou no primeiro semestre de engenharia civil e estou com dificuldades nesse exercício.
Agradeço desde já!
- Anexos
-
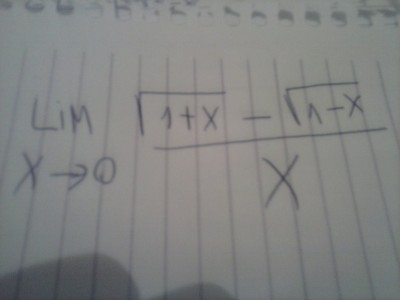
-
Rafael Zanelato
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 31, 2014 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Cleyson007 » Seg Mar 31, 2014 14:29
por Cleyson007 » Seg Mar 31, 2014 14:29
Boa tarde Rafael!
Repare que se você substituir o 0 no numerador e no denominador terá uma indeterminação do tipo 0

. Para que não ocorra a indeterminação, multiplique o numerador e o denominador por
![\sqrt[]{1+x}+\,\sqrt[]{1-x} \sqrt[]{1+x}+\,\sqrt[]{1-x}](/latexrender/pictures/cb67d53382015a30efe8fe6f0058fad1.png)
.
Qualquer dúvida estou a disposição.
Abraço,
Cleyson
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Rafael Zanelato » Seg Mar 31, 2014 16:09
por Rafael Zanelato » Seg Mar 31, 2014 16:09
Boa tarde,
Até ai eu sei chegar, mas eu travo durante essa multiplicação.
Se alguém puder me mandar toda a resolução ficaria grato.
Att,
Rafael Zanelato
-
Rafael Zanelato
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 31, 2014 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Man Utd » Ter Abr 01, 2014 11:28
por Man Utd » Ter Abr 01, 2014 11:28
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LIMITE DE SEQUÊNCIA - ME AJUDEM!!!-
por shallon » Sex Out 23, 2009 20:36
- 1 Respostas
- 2435 Exibições
- Última mensagem por Tom

Sáb Jul 03, 2010 21:30
Sequências
-
- LIMITE DE SEQUÊNCIA - ME AJUDEM!!!-
por shallon » Qua Out 28, 2009 23:47
- 0 Respostas
- 1394 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite modular, me ajudem!
por arthurvct » Ter Abr 23, 2013 14:50
- 3 Respostas
- 1534 Exibições
- Última mensagem por arthurvct

Ter Abr 23, 2013 17:18
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Por favor ajudem
por michelcosta » Dom Nov 17, 2013 10:11
- 0 Respostas
- 536 Exibições
- Última mensagem por michelcosta

Dom Nov 17, 2013 10:11
Cálculo: Limites, Derivadas e Integrais
-
- me ajudem neste exercício de limite
por Claudia Sotero » Sex Nov 20, 2009 16:15
- 2 Respostas
- 4234 Exibições
- Última mensagem por Claudia Sotero

Sáb Nov 21, 2009 10:47
Computação
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Para que não ocorra a indeterminação, multiplique o numerador e o denominador por
. Para que não ocorra a indeterminação, multiplique o numerador e o denominador por ![\sqrt[]{1+x}+\,\sqrt[]{1-x} \sqrt[]{1+x}+\,\sqrt[]{1-x}](/latexrender/pictures/cb67d53382015a30efe8fe6f0058fad1.png) .
.