 por Cleyson007 » Dom Jan 12, 2014 17:11
por Cleyson007 » Dom Jan 12, 2014 17:11
Se um tanque tem 5000 galões de água, que escoa pelo fundo em 40 minutos, então a Lei de Torricelli dá o volume
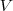
de água que restou no tanque depois de

minutos como
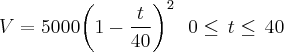
Encontre a taxa segundo a qual a água está escoando do tanque depois de(a) 5 min (b) 10 min (c) 20 min e (d) 40 min. Em que instante o escoamento é mais rápido? E mais vagaroso? Resuma o que você encontrou.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Guilherme Pimentel » Seg Jan 13, 2014 22:43
por Guilherme Pimentel » Seg Jan 13, 2014 22:43
Para ajudar um pouco:
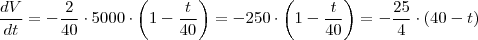
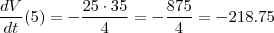
Editado pela última vez por
Guilherme Pimentel em Qua Jan 15, 2014 04:51, em um total de 1 vez.
-
Guilherme Pimentel
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Dom Jan 12, 2014 19:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Economia
- Andamento: formado
 por Cleyson007 » Ter Jan 14, 2014 00:36
por Cleyson007 » Ter Jan 14, 2014 00:36
Olá, boa noite Guilherme!
Amigo, consegui encontrar os valores para 5min, 10min, 20min e 40min. Estou com dúvida nessa parte: "Em que instante o escoamento é mais rápido? E mais vagaroso? Resuma o que você encontrou."
Pode me ajudar?
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Guilherme Pimentel » Qua Jan 15, 2014 04:55
por Guilherme Pimentel » Qua Jan 15, 2014 04:55
Se a pergunta é sobre os tempos nos quais vc calculou a derivada é só comparar os valores obtidos, o de maior valor absoluto é o mais rápido, o de menor valor absoluto é o mais lento.
Se for em relação a todos os momentos possíveis, a resposta é mais rápido em t=0 mais lento em t=40.
-
Guilherme Pimentel
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Dom Jan 12, 2014 19:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Economia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
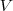 de água que restou no tanque depois de
de água que restou no tanque depois de  minutos como
minutos como 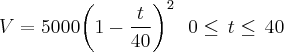



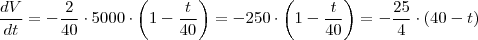
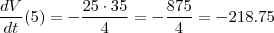



 , avisa que eu resolvo.
, avisa que eu resolvo.

