Está vazando água de um tanque cônico invertido a uma taxa de 10000 cm/min. Ao mesmo tempo, água está sendo bombeada para dentro do tanque a uma taxa constante. O tanque tem 6m de altura e o diâmetro do topo é de 4m. Se o nível da água estiver subindo a uma taxa de 20cm/min quando a altura da água for 2m, encontre a taxa segundo a qual a água está sendo bombeada dentro do tanque.
Alguem da uma luz, pois sei como resolver se não tivesse tanto cano tirando e colocando água =D


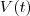 de água no tanque , é a soma do volume inicial
de água no tanque , é a soma do volume inicial 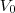 com o volume que entra tanque ,
com o volume que entra tanque , 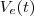 , menos o volume que sai do tanque
, menos o volume que sai do tanque 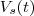 . Isto é ,
. Isto é ,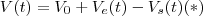 .
.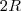 e altura
e altura 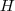 , teremos que o volume de água no tanque
, teremos que o volume de água no tanque 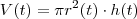 ou de forma equivalente ,
ou de forma equivalente , 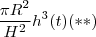 em que
em que 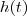 é a altura da água avaliada no instante
é a altura da água avaliada no instante  .Esta última expressão foi obtida por semelhança de triângulos retângulos que fornece
.Esta última expressão foi obtida por semelhança de triângulos retângulos que fornece 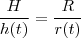 .
. 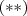 em
em  e derivando com relação a
e derivando com relação a 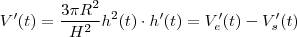 .
. 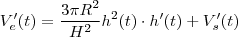 é taxa segundo a qual a água estar sendo bombeada p/ dentro do tanque .
é taxa segundo a qual a água estar sendo bombeada p/ dentro do tanque .
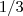 da expressão
da expressão 
 .
.
 :
: