 por Paulo Perez » Sex Out 04, 2013 16:19
por Paulo Perez » Sex Out 04, 2013 16:19
Olá, estou tentando resolver esta integral:
![\int_{}^{}\frac{sen(\sqrt[2]{\Theta})}{\sqrt[2]{\Theta{cos}^{3}(\sqrt[2]{\Theta})}}d\Theta \int_{}^{}\frac{sen(\sqrt[2]{\Theta})}{\sqrt[2]{\Theta{cos}^{3}(\sqrt[2]{\Theta})}}d\Theta](/latexrender/pictures/0ba7921d3d811e84af15cfe9d3b174af.png)
porém, a lista de exercício não apresenta resposta e eu cheguei neste resultado pelo método da substituição e por partes:
![\frac{4}{3}tg(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-\frac{8}{27}{sec}^{\frac{9}{2}}(\sqrt[2]{\Theta}) \frac{4}{3}tg(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-\frac{8}{27}{sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})](/latexrender/pictures/c17c350e95eb03768bdc4584370b4ce5.png)
como não fiquei satisfeito em não saber se estava correto, tirei a prova real, derivando o resultado obtido acima cheguei em:
![\frac{3{tg}^{2}(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-2tg(\sqrt[2]{\Theta}){sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})+2{sec}^{\frac{7}{2}}(\sqrt[2]{\Theta})}{3\sqrt[2]{\Theta}} \frac{3{tg}^{2}(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-2tg(\sqrt[2]{\Theta}){sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})+2{sec}^{\frac{7}{2}}(\sqrt[2]{\Theta})}{3\sqrt[2]{\Theta}}](/latexrender/pictures/a0f59f149fdb92e96c700186e6db8822.png)
e pela "pequena" diferença entre a função original e a prova real conclui que estava errado (ah vá!) e agora peço ajuda para vocês, porque não tenho a mínima ideia de como resolver este exercício.
Obrigado
-
Paulo Perez
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 03, 2013 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sáb Out 05, 2013 10:10
por young_jedi » Sáb Out 05, 2013 10:10
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL] Integral Impossível... =S
por antonelli2006 » Qua Abr 25, 2012 00:40
- 1 Respostas
- 1973 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 15:50
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4622 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4590 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4348 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2848 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{sen(\sqrt[2]{\Theta})}{\sqrt[2]{\Theta{cos}^{3}(\sqrt[2]{\Theta})}}d\Theta \int_{}^{}\frac{sen(\sqrt[2]{\Theta})}{\sqrt[2]{\Theta{cos}^{3}(\sqrt[2]{\Theta})}}d\Theta](/latexrender/pictures/0ba7921d3d811e84af15cfe9d3b174af.png)
![\frac{4}{3}tg(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-\frac{8}{27}{sec}^{\frac{9}{2}}(\sqrt[2]{\Theta}) \frac{4}{3}tg(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-\frac{8}{27}{sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})](/latexrender/pictures/c17c350e95eb03768bdc4584370b4ce5.png)
![\frac{3{tg}^{2}(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-2tg(\sqrt[2]{\Theta}){sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})+2{sec}^{\frac{7}{2}}(\sqrt[2]{\Theta})}{3\sqrt[2]{\Theta}} \frac{3{tg}^{2}(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-2tg(\sqrt[2]{\Theta}){sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})+2{sec}^{\frac{7}{2}}(\sqrt[2]{\Theta})}{3\sqrt[2]{\Theta}}](/latexrender/pictures/a0f59f149fdb92e96c700186e6db8822.png)


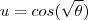
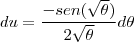
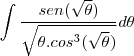
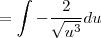
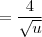
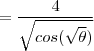

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.