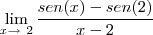
Eu tenho dúvida quanto a simplificação para o -lim sen(2), neste limite.
Pensei inicialmente que havia obtido o valor correto para as operações, mas percebi que estava enganado quanto a simplificação de -sen(2), então queria simplesmente que me dissessem o caminho para poder realizar esta simplificação.
Quando estava a resolver anteriormente já havia incluído o uso de uma variável y de modo que y=x-2 tal que x=y+2 e logo
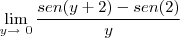
A resposta dada para a questão segundo a lista é cos(2).
Obrigado pelo seu tempo.
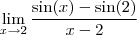
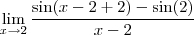
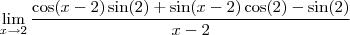
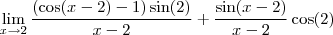
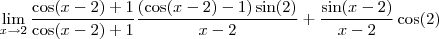
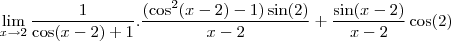
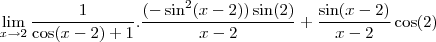
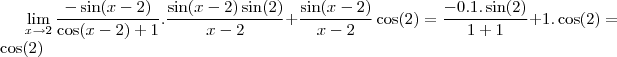
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)