Nicolas1Lane escreveu: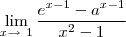
=
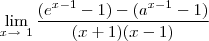
Bom, quando trabalhamos com limites, normalmente o primeiro passo que damos é tentar "fatorar" o limite, para que fique mais fácil de se trabalhar e enxergar o que acontece. E foi isso o que aconteceu com o limite acima.
No numerador, foi somado (-1) à todos os membros. Repare que -1-(-1)=0, então o que foi acrescentado no numerador, não altera em nada a função.Mas lembre-se de que quando utilizar esta "ferramenta", deve ser em todos os membros, senão a função original será alterada e, com isso, o resultado será alterado. E no denominador, houve a decomposição do número do número,onde (x+1)(x-1) = x² - x + x - 1 = x²+1. Repare que foi empregada a propriedade da distributiva.
Essas são ferramentas muito usadas no estudo de limites. Aconselho você pegar mais exemplos de exercícios de limites. Pois quanto mais fizer, mais fácil ficará e, no final, você utilizará esses "macetes" sem perceber.
Espero ter ajudado!
Abraços
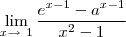
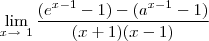


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.