 por Pessoa Estranha » Qui Ago 22, 2013 17:18
por Pessoa Estranha » Qui Ago 22, 2013 17:18
Olá pessoal, gostaria de ajuda para calcular o seguinte limite.
É um exercício que pede para usar a regra de L´Hospital.
Pensei que pudesse ser um caso de função limitada e então, o resultado seria o limite do sen(x), mas fiquei insegura com relação a isto. Contudo, ao tentar usar a regra de L´Hospital, tentei transformar a "expressão" num quociente e então, aplicar a regra; mas não ajudou em nada.
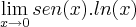
(x tende a zero pela direita).
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por temujin » Qui Ago 22, 2013 19:11
por temujin » Qui Ago 22, 2013 19:11
Tente escrever a fração como:
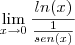
E agora aplique l'Hospital (lembre-se que no denominador vc tem que usar a regra da cadeia):
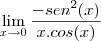
Aplicando l'Hospital de novo:
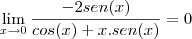
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por Pessoa Estranha » Qui Ago 22, 2013 23:13
por Pessoa Estranha » Qui Ago 22, 2013 23:13
Obrigada por responder! Bom, seguindo a sua sugestão, a minha resolução ficaria assim:
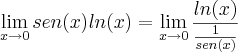
Como trata-se de uma indeterminação e conseguimos reescrever o limite num quociente, podemos aplicar L´Hospital.
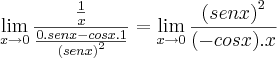
Novamente obtemos uma indeterminação, então:
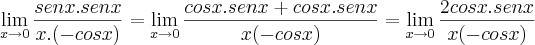
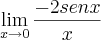
Indeterminação, então:
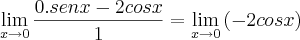
= -2.
Eu sei que está errado, mas qual é o meu erro?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por temujin » Sex Ago 23, 2013 00:06
por temujin » Sex Ago 23, 2013 00:06
Olá.
O problema está na segunda indeterminação. No numerador vc tem

.
Pra facilitar, faça uma substituição:
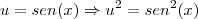
Derivando:
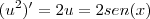
Além disto, no denominador vc tem
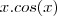
, que tb precisa ser derivado (regra do produto):
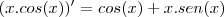
Portanto, o limite fica:
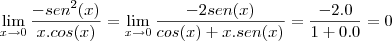
Não sei se ficou mto claro, qualquer dúvida é só perguntar.

-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por e8group » Sex Ago 23, 2013 00:52
por e8group » Sex Ago 23, 2013 00:52
Pensei de outra forma ,espero que esteja certo .
Escolhendo um
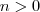
de modo que
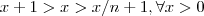
. Como a função
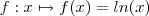
é injetora (ela é estritamente crescente) então
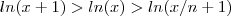
e portanto
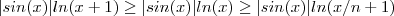
ocorrendo a igualdade somente quando
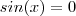
para

. Como
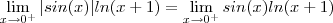
e além disso ,
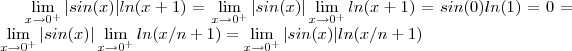
.
Logo , pelo teorema do confronto
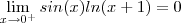
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Ago 23, 2013 01:01
por e8group » Sex Ago 23, 2013 01:01
Agora que percebi ,a solução acima torna invalida para
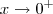
pois
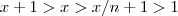
.Por favor desconsiderem .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Sex Ago 23, 2013 15:02
por Pessoa Estranha » Sex Ago 23, 2013 15:02
Obrigada por terem respondido.
Eu entendo que facilitaria bastante se substituir
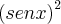
por uma variável

; contudo, não posso aplicar a regra do produto?
Eu pensei assim:
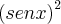
=
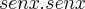
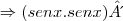
=
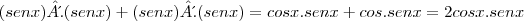
.
(ingnorem estes Â)
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Sex Ago 23, 2013 15:17
por Pessoa Estranha » Sex Ago 23, 2013 15:17
Percebi algo agora....
Na minha resolução (lá em cima), eu acho que esqueci de derivar o denominador (preocupei-me em derivar o numerador, mas esqueci do outro).
Vamos ver:
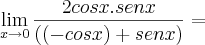
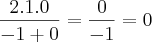
.
Vejam!!!! Bom, esta resolução só pode estar certa se estiver correto aplicar a regra do produto em
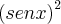
. Pode?
Já pensou em esquecer de derivar o denominador na prova de Cálculo????!!!!

Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Man Utd » Sáb Ago 24, 2013 15:28
por Man Utd » Sáb Ago 24, 2013 15:28
Pessoa Estranha escreveu:Eu entendo que facilitaria bastante se substituir
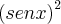
por uma variável

; contudo, não posso aplicar a regra do produto?
pode sim

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5411 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4759 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4786 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4812 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2794 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
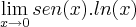


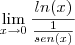
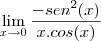
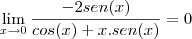

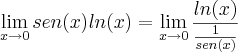
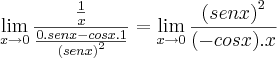
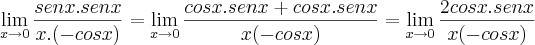
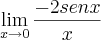
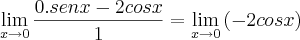
 .
. 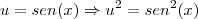
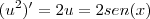
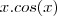 , que tb precisa ser derivado (regra do produto):
, que tb precisa ser derivado (regra do produto):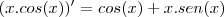
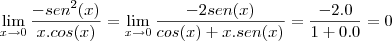

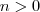 de modo que
de modo que 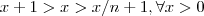 . Como a função
. Como a função 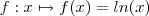 é injetora (ela é estritamente crescente) então
é injetora (ela é estritamente crescente) então 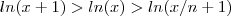 e portanto
e portanto 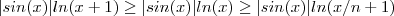 ocorrendo a igualdade somente quando
ocorrendo a igualdade somente quando 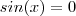 para
para  . Como
. Como 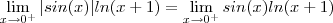 e além disso ,
e além disso , 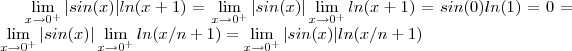 .
.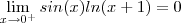 .
.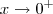 pois
pois 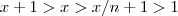 .Por favor desconsiderem .
.Por favor desconsiderem .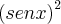 por uma variável
por uma variável  ; contudo, não posso aplicar a regra do produto?
; contudo, não posso aplicar a regra do produto?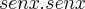
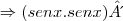 =
= 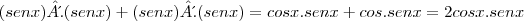 .
.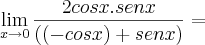
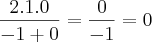 .
.




