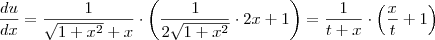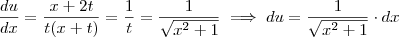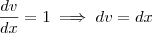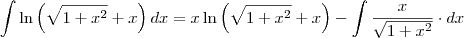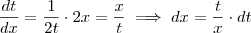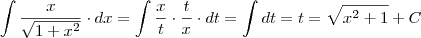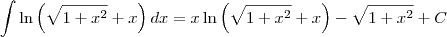por armando » Ter Jul 23, 2013 19:38
por armando » Ter Jul 23, 2013 19:38
Olá pessoal.
Como resolver o seguinte Integral:
O que faço com aquele
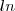
?
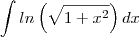
Grato
armando
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Ter Jul 23, 2013 22:01
por MateusL » Ter Jul 23, 2013 22:01
Armando,
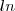
é o logarítmo natural.
Procurando em uma tábua de integrais:
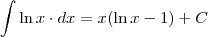
Mas terás que fazer uma substituição para resolver a integral que escrevestes.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por armando » Dom Jul 28, 2013 21:46
por armando » Dom Jul 28, 2013 21:46
Oi MateusL
Pode me explicar como fica essa substituição ? É que estou aprendendo esta matéria, e esse negócio da substituição ainda é muito confuso pra mim.
Coloquei a questão no WolframAlpha, no dispositivo de resolução step by step, e me deu como solução:
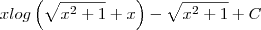
Não deveria ser
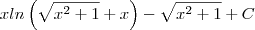
Nota__ Contudo, no fim, após a solução diz :
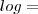 Logaritmo natural»
Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
Grato:
armando
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Dom Jul 28, 2013 23:31
por MateusL » Dom Jul 28, 2013 23:31
Olá Armando.
O

no Wolfram é a mesma coisa que o
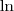
. Notações diferentes para a mesma coisa.
A integral que encontrastes é a integral da função
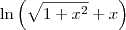
, mas no enunciado escrevestes
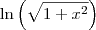
.
Agora fiquei na dúvida de qual função você quer descobrir a integral:
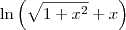
ou
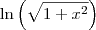
?
Ah, acho que me enganei quando disse que deverias resolver por substituição.
Acredito que terás que resolver por partes.
Abraço
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por armando » Seg Jul 29, 2013 11:15
por armando » Seg Jul 29, 2013 11:15
Oi MateusL
Desculpe, de facto, o enunciado correto é o da ultima versão.
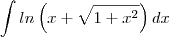
Obrigado pelo reparo.
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Seg Jul 29, 2013 14:48
por MateusL » Seg Jul 29, 2013 14:48
Então vamos à resolução:
Pela integração por partes, sabemos que:
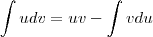
Façamos:
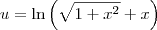

Então
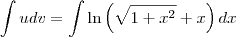
Teremos, fazendo
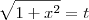
para facilitar a notação:
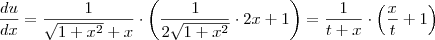
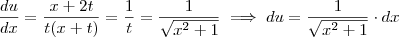
E também:
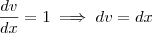
Assim:
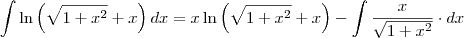
Notemos que:
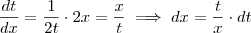
Então:
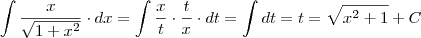
Portanto:
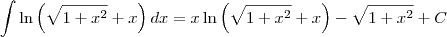
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ?
?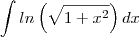

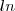 ?
?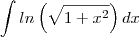

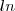 é o logarítmo natural.
é o logarítmo natural.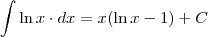

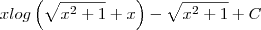
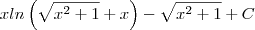
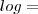 Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
 no Wolfram é a mesma coisa que o
no Wolfram é a mesma coisa que o 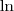 . Notações diferentes para a mesma coisa.
. Notações diferentes para a mesma coisa.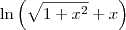 , mas no enunciado escrevestes
, mas no enunciado escrevestes 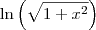 .
.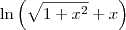 ou
ou 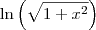 ?
?
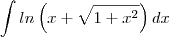

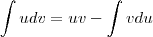
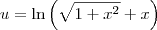

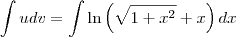
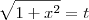 para facilitar a notação:
para facilitar a notação: