Como resolver o seguinte Integral:
O que faço com aquele
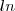 ?
?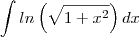
Grato
armando

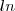 ?
?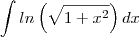

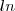 é o logarítmo natural.
é o logarítmo natural.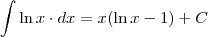

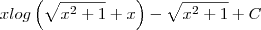
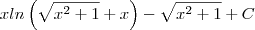
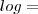 Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
 no Wolfram é a mesma coisa que o
no Wolfram é a mesma coisa que o 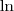 . Notações diferentes para a mesma coisa.
. Notações diferentes para a mesma coisa.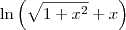 , mas no enunciado escrevestes
, mas no enunciado escrevestes 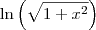 .
.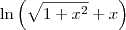 ou
ou 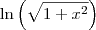 ?
?
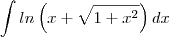

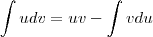
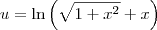

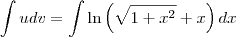
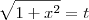 para facilitar a notação:
para facilitar a notação: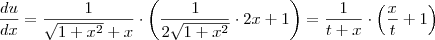
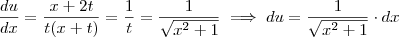
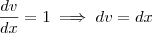
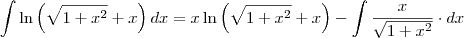
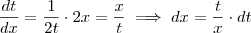
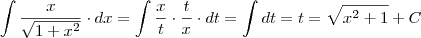
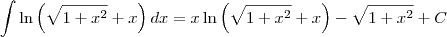

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes