


 de cada função do denominador e numerador após calcular seus limites . Observe que para
de cada função do denominador e numerador após calcular seus limites . Observe que para  vale a expressão que é equivalente a mesma postada:
vale a expressão que é equivalente a mesma postada: 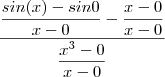 . Tomando o limite com
. Tomando o limite com 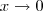 e utilizando suas regras operatórias , obtemos:
e utilizando suas regras operatórias , obtemos: 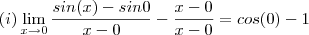 que devido a continuidade de
que devido a continuidade de 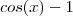 no ponto
no ponto  ,segue
,segue 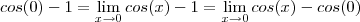 .
.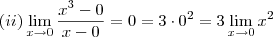 (Por quê ??)
(Por quê ??) 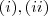 vemos que
vemos que 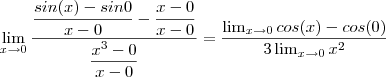 .Muliplicando o denominador e numerador por
.Muliplicando o denominador e numerador por  e seguindo o mesmo raciocínio utilizado nos itens acima , você obterá como resposta
e seguindo o mesmo raciocínio utilizado nos itens acima , você obterá como resposta 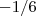 .
. 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
